这篇文章上次修改于 231 天前,可能其部分内容已经发生变化,如有疑问可询问作者。
算法四:支持向量机
概述
支持向量机(Support Vector Machine,SVM)算法应用广泛,可以分类,可以回归。
在处理二元分类上:
- 支持向量机与逻辑回归的决策边界一样是线性的(支持向量机做的更好)
- 学习方式:以间隔最大化为基准,让决策边界尽可能地远离数据。
- 间隔:训练数据中,最接近决策边界的数据与决策边界之间的距离
示例代码
from sklearn.svm import LinearSVC
from sklearn.datasets import make_blobs
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
centers = [(-1, -0.125), (0.5, 0.5)]
X, y = make_blobs(n_samples=50, n_features=2, centers=centers, cluster_std=0.3)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3)
model = LinearSVC()
model.fit(X_train, y_train) # 训练
y_pred = model.predict(X_test)
accuracy_score(y_pred, y_test) # 评估详细说明
如果数据不一定是线性分离的,也就是两类的数据点可能交杂在一起。
- 间隔内侧:指的是一些数据点会落在决策边界的“间隔”之内,甚至可能越过决策边界进入另一侧。这种情况下,这些数据点被称为“间隔内侧数据点”
- 硬间隔:适用于线性可分的数据,不允许任何数据点进入间隔内侧或越过决策边界,即要求分类严格无误。
- 软间隔:适用于数据可能非线性可分的情况,允许部分数据点进入间隔内侧甚至越界。这种方法使用松弛变量允许少量错误分类,以便在复杂的数据集上找到更好的决策边界。
以下考虑软间隔
设D为点与决策边界之间的距离;基于学习结果,我们可以将训练数据分为以下3种:
- D > 间隔:间隔外侧的数据。
- D = 间隔:间隔上的数据。
- D < 间隔,或者误分类的数据:间隔内侧的数据。
将D ≤ 间隔的数据称为支持向量,确定了决策边界,间隔外侧的数据则不会影响决策边界。
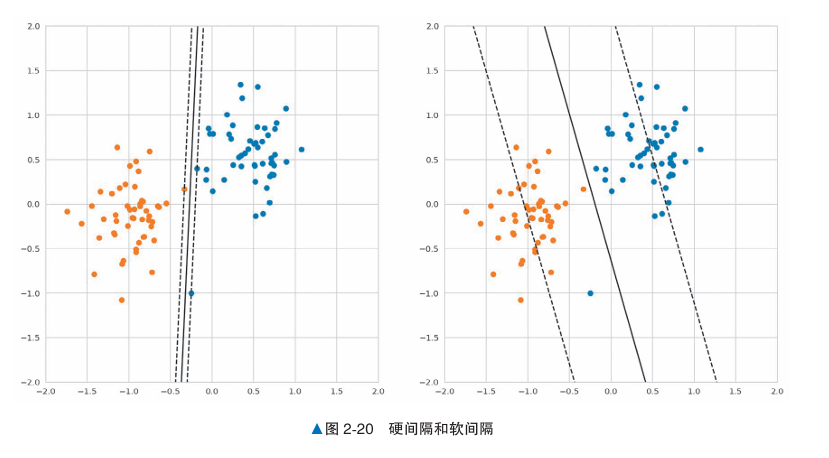
对于以上例子,对于线性可分的数据,如果强制训练数据不进入间隔内侧,可能会导致学习结果对数据过拟合。
在使用软间隔时,允许间隔内侧进入多少数据由超参数决定。
与其他算法一样,在决定超参数时,需要使用网格搜索(grid search)和随机搜索(random search)等方法反复验证后再做决定。
算法五:支持向量机(核方法)
概述
在支持向量机中引入核方法(kernel methods)这个技巧,那些无法人力标注特征值的复杂 数据也能被处理。当然,这个算法现在也用于解决各种分类和回归问题。
对于支持向量机来说,如果数据是以中心,外围的模式分成两组,直线的决策边界就无法进行处理。
算法说明
核方法的一个常见解释是“将数据移动到另一个特征空间,然后进行线性回归”。
将线性不可分的数据变为线性可分的一种方法是引入更高维度的空间。
通过在更高维空间中表示训练数据,每个原始数据点可以映射成高维空间中的一个点,这些点在高维空间中是线性可分的。此时,支持向量机可以在高维空间中找到适合的决策边界。然后将该决策边界投影回原始的低维空间,就得到了一个可以有效分类的边界。
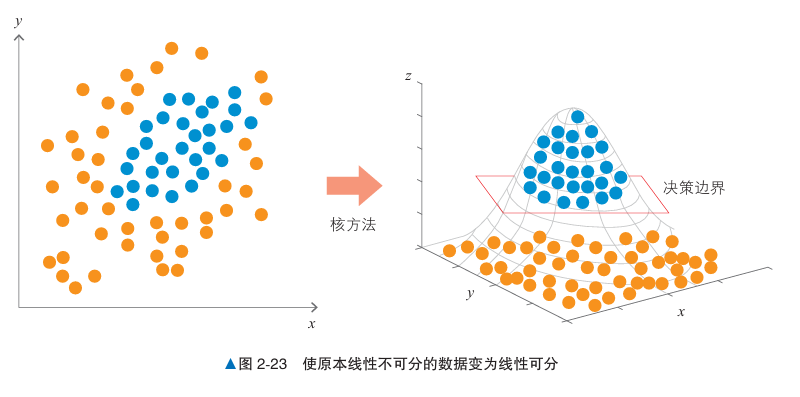
虽然构建线性分离的高维空间非常困难,但通过一个叫作核函数的函数,核方法就可以使用在 高维空间中学习到的决策边界,而无须构建具体的线性分离的高维空间。
示例代码
from sklearn.svm import SVC
from sklearn.datasets import make_gaussian_quantiles
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
# 生成数据
X, y = make_gaussian_quantiles(n_features=2, n_classes=2, n_samples=300)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3)
model = SVC()
model.fit(X_train, y_train)
y_pred = model.predict(X_test)
accuracy_score(y_pred, y_test)详细说明
核方法中可以使用的核函数多种多样。使用不同的核函数,得到的决策边界的形状也不同。
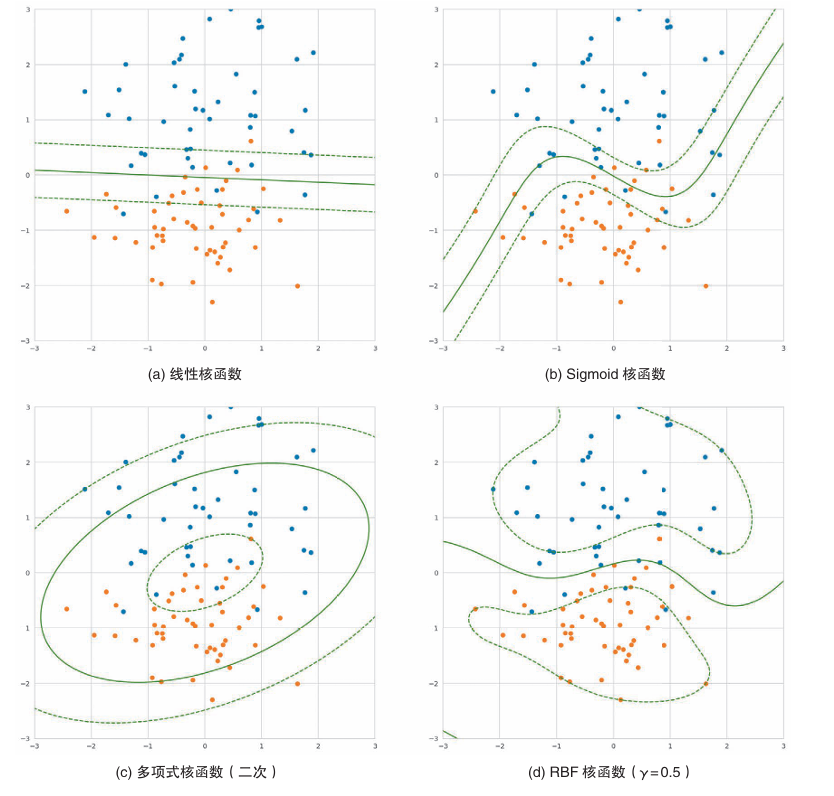
因此可以知道,在不同的核函数下,可以进行不同的甚至更复杂的决策边界分割。
由于这些特点,在使用支持向量机时,不宜立即使用非线性核函数,在此之前,应先使用线性核函数进行分析,以了解数据。
算法六:朴素贝叶斯
概述
朴素贝叶斯(Naive Bayes)是常用于自然语言分类问题的算法。其计算数据为某个标签的概率,并将其分类为概率值最大的标签。
根据词频进行分类,也就是自然语言中,根据文本中内容不同类型词频,来判断这个文本属于哪个类别。
在预测数据类别时,朴素贝叶斯会计算特定单词在各个类别中的条件概率。
例如,对于验证数据中的“感动”一词,虽然在不同类别(如“电影”和“宇宙”)都会出现,但在每个类别中出现的概率不同:感动在电影的三条数据中出现两次,在宇宙的三条数据中只出现一次。
这表明“感动”一词在“电影”类别中更常见。
并且,还记录了条件概率:在出现某个标签的情况下,为某个类型的概率
例如:在出现了“感动”一词的情况下,是电影的概率是66%
朴素贝叶斯综合利用文本中每个单词的条件概率,假设单词的出现是相互独立的,即一个单词的出现不会影响其他单词的出现概率。
最终,通过单词的条件概率累积,求出文本在不同类别下的概率值,将文本归到概率最高的类别。
算法说明
预处理
BoW(Bag of Words)词袋:由特征值构成的向量和标签的组合。
先从现有的训练数据的文本中只提取出名词,忽略名词在文本中的顺序,把它们作为集合,作为列名
每一条训练数据都可以看做一行数据(向量),对应了每个列名出现的次数。
假设我们有两段短文本:
- “我喜欢机器学习”
- “机器学习很有趣”
首先,我们对这两段文本进行分词:
- 文本 1 分词结果:
["我", "喜欢", "机器", "学习"] - 文本 2 分词结果:
["机器", "学习", "很", "有趣"]
创建词汇表:
接着,我们把所有的词汇都列出来,形成一个词汇表:
["我", "喜欢", "机器", "学习", "很", "有趣"]生成词频向量:
然后,我们可以用这个词汇表来表示每一段文本,通过记录词汇表中每个词在该文本中出现的次数(即词频)来生成向量表示。
- 文本 1 的向量:
[1, 1, 1, 1, 0, 0] - 文本 2 的向量:
[0, 0, 1, 1, 1, 1]
概率的计算
在分类时求出每个标签对应的概率,将概率最高的标签作为分类结果。朴素贝叶斯在训练时计算以下两种概率。
- 每个标签(类型)出现的概率。
- 在各标签(类型)下,每个单词出现的条件概率。
平滑:是一种平衡的方式,将没有出现的单词概率0改为小的概率值如:0.01
朴素贝叶斯认为所有词的出现都是独立事件:
因此分别为每个标签值计算每个标签条件概率的乘积
代码
from sklearn.naive_bayes import MultinomialNB
# 生成数据
X_train = [[1, 1, 0, 0, 0, 1, 0, 0, 0, 0, 0],
[0, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0],
[1, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 0],
[0, 0, 0, 0, 0, 1, 1, 1, 0, 0, 1]]
y_train = [1, 1, 1, 0, 0, 0]
model = MultinomialNB()
# 训练
model.fit(X_train, y_train)
# 预测新数据
y_pred = model.predict(X_train)
y_pred_prob = model.predict_proba(X_train)
model.predict([[1, 1, 0, 0, 0, 1, 0, 0, 0, 0, 0]])详细说明
朴素贝叶斯是自然语言分类的基础算法,但是不适合预测天气预报中的降水概率那种预测值是概率本身的情况。
朴素贝叶斯所有词的出现都是独立事件,忽略了单词之间的关联性,若单词关联性强,应当考虑其他模型果的影响方向和程度。