这篇文章上次修改于 221 天前,可能其部分内容已经发生变化,如有疑问可询问作者。
算法七:随机森林
概述
随机森林通过多个决策树模型来共同解决问题的算法。单个决策树的性能不一定够高,由多个决策树多数表决得到的结果能有更高的预测精度。
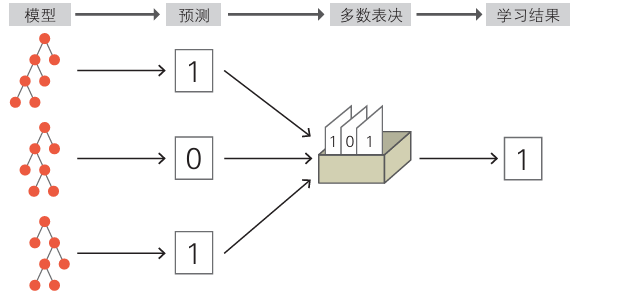
如果每个决策树的结果相同,那么最后的表决结果也不会有变化,所以每个决策树要具备多样性,以下介绍。
算法说明
决策树
决策树是将训练数据进行划分的方法。
决策树的输入通常是 特征矩阵 与 标签向量,相当于数据内容和分类结果。
训练数据的杂乱程度称为不纯度。利用不纯度来比较分割方法的优劣。
表示不纯度的具体指标有很多,如基尼系数。
基尼系数 = (c是标签数,pi是某标签的数量在总数的占比)
所示为使用几种不同的分割方法计算得出的 加权平均基尼系数(区域内的基尼系数乘以区域在总数占比)
左侧是分割前的状态。右侧是使基尼系数的平均值最小的分割方法的例子。
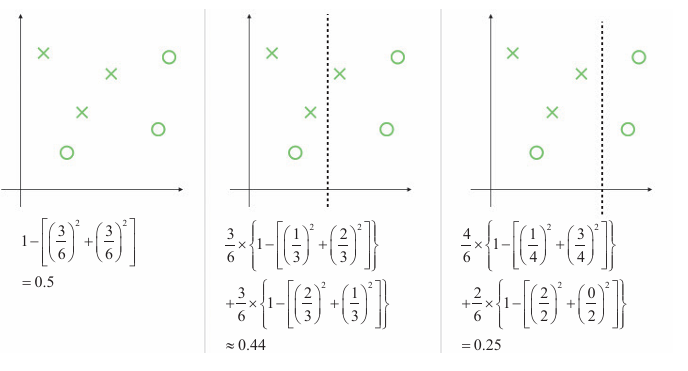
决策树便是通过反复分割来进行的。
步骤:
-
计算某个区域的所有特征值和候选分割的不纯度.
-
以分割时不纯度减小最多的分割方式分割区域。
-
对于分割后的区域,重复步骤1和步骤2。
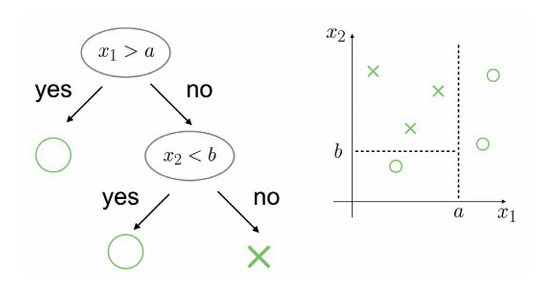
随机森林
随机森林如何使用多个决策树来提高正确率:
- 假设每个决策树的正确率都是60%
- 对于训练后决策树,每次的输入都会给定一个答案,n个决策树都给出正确率为60%的答案
- 服从多数正确,最后的正确率会大于60%
决策树如何在相同数据下独立:
-
Bootstrap方法:每个决策树获得的样本集是 n 次的 有放回的随机抽取 集合(也就是单个数据可能重复)。
-
随机选取特征值:对于每个节点的分裂,不使用全部特征,而是随机选择一个特征子集来决定分裂。
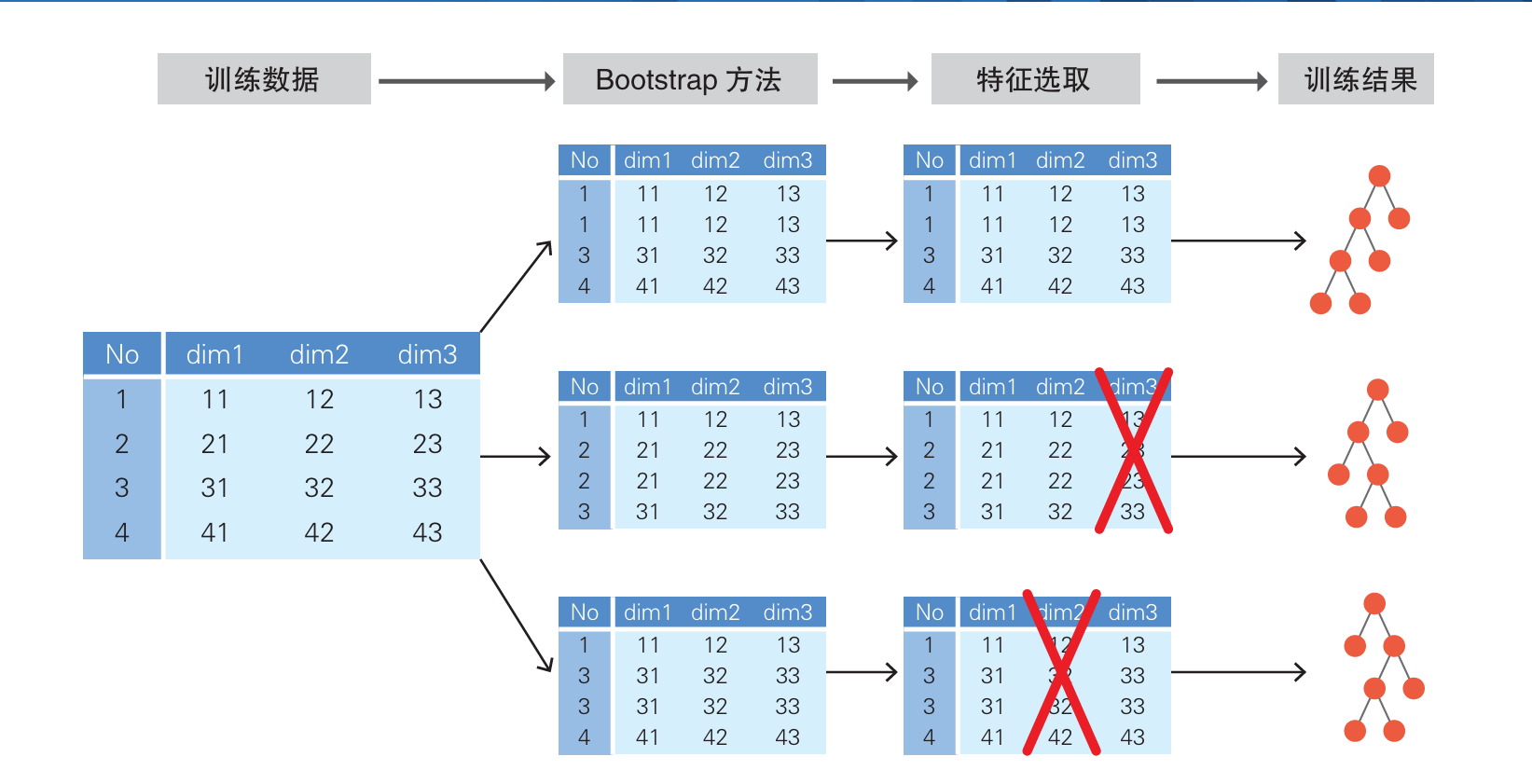
随机森林利用这种方式创建多棵数据集、训练多棵决策树、对预测结果进行多数表决,返回最终的分类结果。
示例代码
用随机森林基于3种葡萄酒的各种测量值数据,对葡萄酒进行分类。
from sklearn.datasets import load_wine
from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
# 读取数据
data = load_wine()
X_train, X_test, y_train, y_test = train_test_split(
data.data, data.target, test_size=0.3)
model = RandomForestClassifier()
model.fit(X_train, y_train) # 训练
y_pred = model.predict(X_test)
accuracy_score(y_pred, y_test) # 评估详细说明
特征的重要度
随机森林可以让我们知道每个特征对预测结果的重要度(影响大小)。
通过对随机森林的所有决策树求在以某个特征分割时的不纯度并取平均值,可以得到特征的重要度。
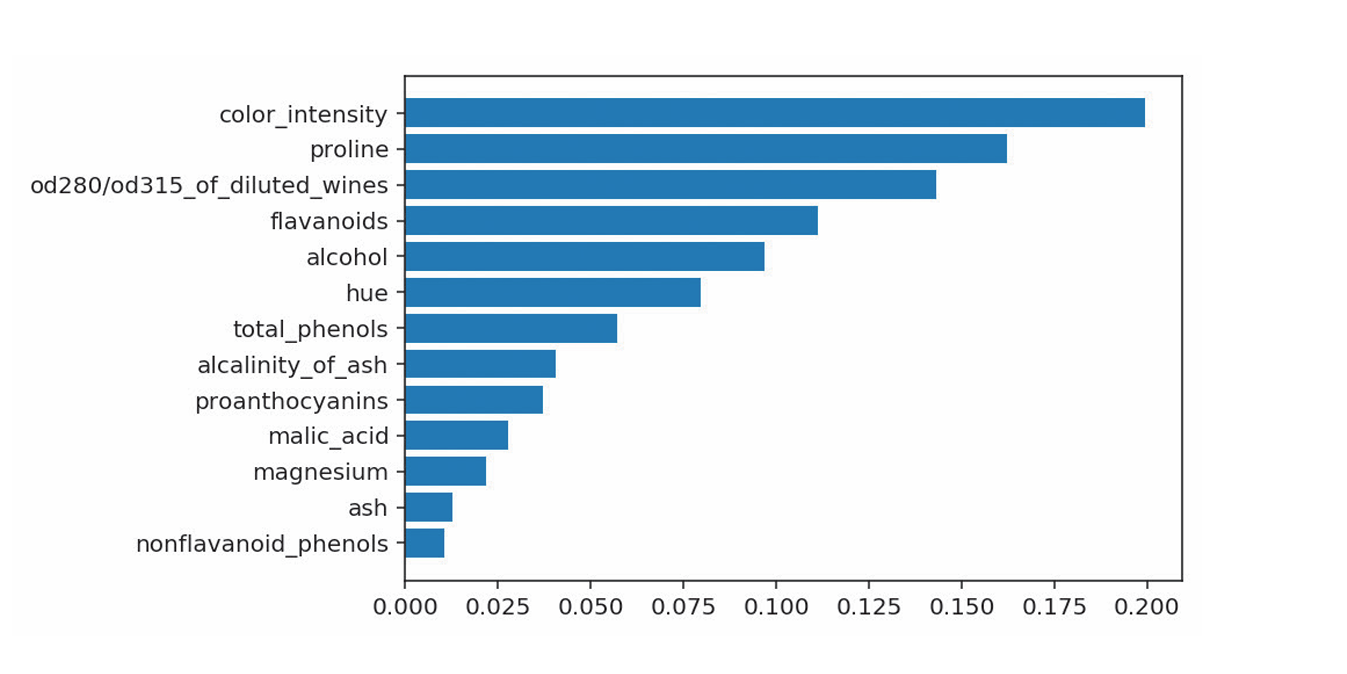
将重要度高的特征用于分割,有望大幅度减小不纯度。反之,重要度低的特征即使被用于分割,也无法减小不纯度,所以可以说这样的特征是非必要的。基于特征的重要度,我们可以去除非必要的特征。
下图为使用随机森林算出的葡萄酒分类中的特征重要度,重要度最高的特征color_intensity表示色泽对葡萄酒分类非常重要。
算法八 神经网络
概述
神经网络由输入层、中间层、输出层组成,常用于分类问题。其中中间层最为重要,能够学习复杂的决策边界。
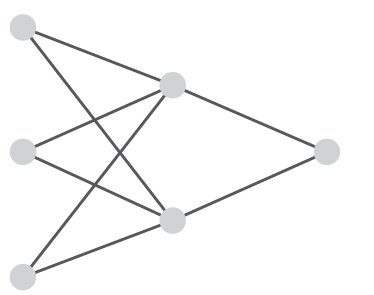
如图为典型的神经网络的的网络结构。其中左侧输入层为三维数据,是输入数据本身,中间层为二维,右侧输出层为一维,取输入数据分类结果的概率。

如图为一个具体例子,对一个叫做MNIST的手写数字数据集进行分类,其中包含0到9十个手写数字的8*8的灰度图片。
下图为MNIST的神经网络示意图(忽略了各节点连线)
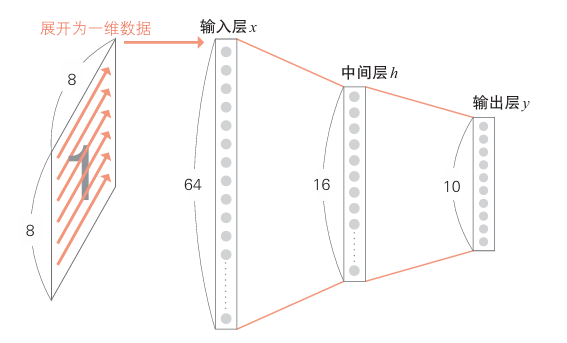
对于8x8的图像,左侧输入层将各个点的像素值存储在长度为64的一维数组中,可视为64维。
中间层使用Sigmoid 等非线性函数计算输入层传来的数据,设置为16维。
输出层也使用非线性函数计算中间层传来的数据。
输出图像是0~9这十个数字的概率。
算法说明
简单感知机
简单感知机由输入层和输出层构成,是将非线性函数应用于对特征值加权后的结果并进行识别的模型。它的工作原理基于加权求和和阶跃函数
举例:某特征维度为2,输入特征值为,使用非线性函数 f 计算概率 y :
- 加权求和:特征值的系数w1和w2称为 权重,常数项w0称为偏置。
- 激活函数:例如Sigmoid 可以将加权值转为一个概率值,通常激活函数后的输出通常是一个连续值,Sigmoid适合二值分类,如果要多分类,Softmax函数将更适合。
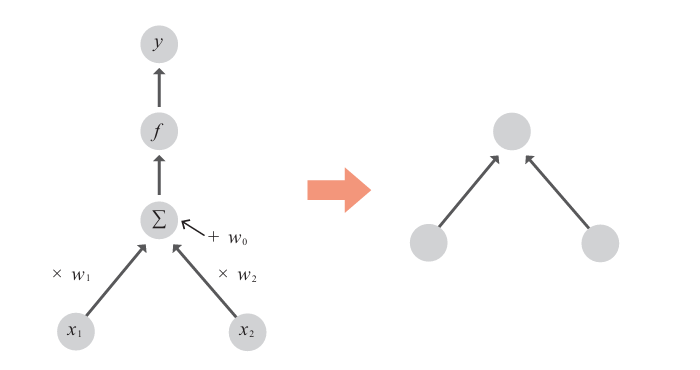
图中是简单感知机的示意图,右图为简化图。
对于感知机的权值确定,感知机的权重在理想情况下在多次训练后会逐渐收敛到一个能够完美分割数据的解,前提是训练数据是线性可分的。如果数据是线性可分的,感知机算法保证最终会收敛。
神经网路
神经网络(Neural Network)可以看作是由多个感知机(Perceptron)通过分层构建而成的。
简单感知机不能很好学习某些数据的决策边界,如下图,典型的数据不是线性可分。
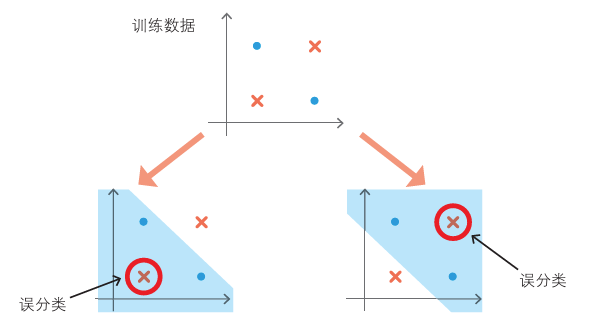
于是我们需要借用多个感知机,并进行一些处理。进行一个分层:
对这个例子 设置两个中间层
- 区分右上角的点和其他点的层
- 区分左下角的点和其他点的层
然后,设置综合这两个输出结果,同样利用简单感知机生成最终决定的层。通过这种做法,我们就可以根据数据是否进入被两条直线夹住的地方来分类了。示意图如下。
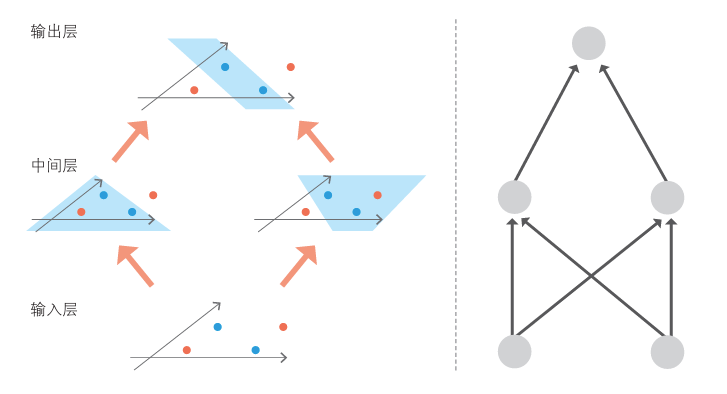
通过调节中间层的数量及层的深度可以学习更复杂的边界。如图。
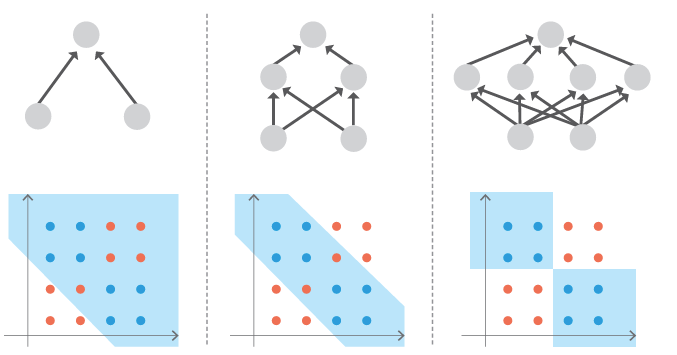
示例代码
from sklearn.datasets import load_digits
from sklearn.neural_network import MLPClassifier
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
# 读取数据
data = load_digits()
X = data.images.reshape(len(data.images), -1)
y = data.target
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3)
model = model = MLPClassifier(hidden_layer_sizes=(16, ))
model.fit(X_train, y_train) # 训练
y_pred = model.predict(X_test)
accuracy_score(y_pred, y_test) # 评估详细说明
模型复杂之后容易过拟合。Early Stopping这种方法可以防止过拟合。
Early Stopping
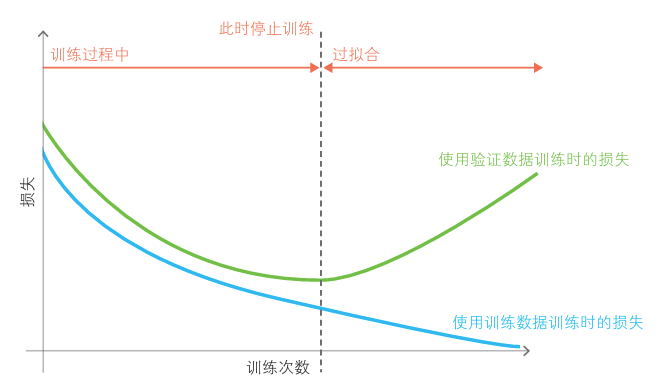
早停法指进入过拟合之前停止训练来防止过拟合。
它进一步划分训练数据,将其中一部分作为训练中的评估数据。在训练过程中据此以此记录损失等评估指标,以了解训练的进度。如果损失开始恶化,出现过拟合的趋势,则停止训练。
算法九:KNN
概述
KNN独特于它只是机械地记住所有数据。
KNN不用进行训练和预测的复杂过程。或者说在训练过程无计算,在预测过程中计算。
在分类未知数据时,KNN将计算未知数据与训练数据的距离,通过多数表决找到最邻近的个点,然后进行分类。
其虽然简单,但能适用于具有复杂边界的数据,如图。
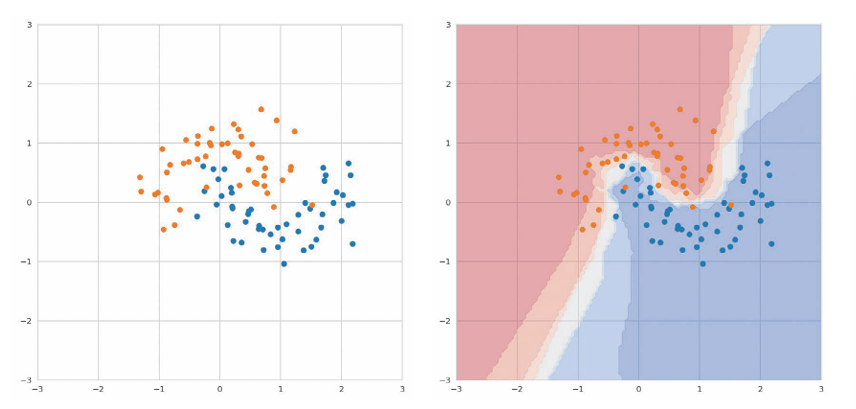
右图中,散点图中所有点被分为两个标签,分类结果表示为热图。
最近邻点的数量k设置为5,给出一个预测数据,找到这个预测数据在输入数据中最近的5个点判断。
图中每个坐标的颜色表示k个最近邻标签的占比。
暗红色区域表示k个点的标签是橙色的,随着比例接近1:1,颜色会变浅,接近于蓝色。
算法说明
KNN算法步骤如下:
-
计算输入数据与训练数据之间的距离。
-
得到距离输入数据最近的k个训练数据。
-
对训练数据的标签进行多数表决,将结果作为分类结果。
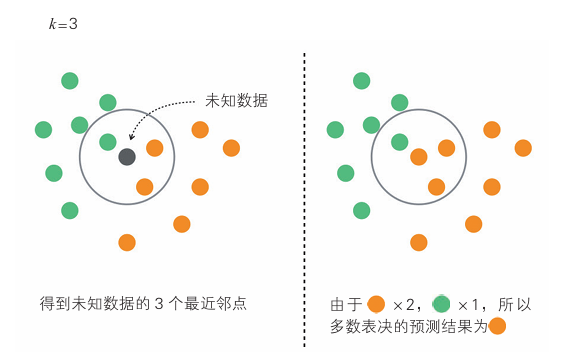
如图,图中 设置的最近邻点k的数量为3。最近邻点k的数量是一个超参数,在二元分类时,通常取为奇数,便于多数表决。
示例代码
样本数据呈曲线分布,最近邻点k的数量采用默认值5.
from sklearn.neighbors import KNeighborsClassifier
from sklearn.datasets import make_moons
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
# 生成数据
X, y = make_moons(noise=0.3)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3)
model = KNeighborsClassifier()
model.fit(X_train, y_train) # 训练
y_pred = model.predict(X_test)
accuracy_score(y_pred, y_test) # 评估详细说明
决策边界因k值而异
k 值低更容易导致 过拟合,而 k 值高则可能导致 欠拟合。
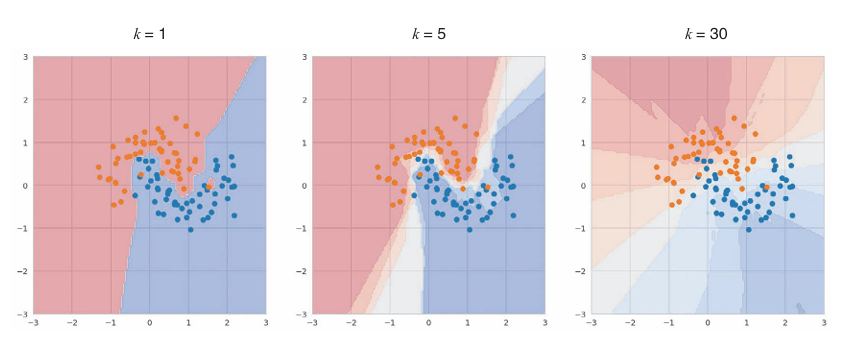
图中从左到右分别为 k=1、5、30。
k=1时出现了像飞地一样的决策边界,说明发生了过拟合。过少的k值可能会使模型非常敏感于训练数据中的噪声和异常值。
k=5时边界变得平滑,相比于 k=1明显好转。
而k=30时,在橙色区域夹杂了许多蓝色的点,说明边界过于宽松导致 错误的判断。它会更多地依赖于全局模式而非局部数据。这样,模型可能无法捕捉到数据中的细节和复杂性
以上说明k值十分重要,需要调优得到最佳的k值。
注意点
数据量较小或维度较小时,KNN效果很好。但是一旦数据量较大或维度较大,KNN需要在大量训练数据进行近邻搜索以找到最近的点。需要大量存储容量来存储数据。因此不适合 KNN。
对于高维数据,KNN也无法很好学习。KNN起作用的前提是“只要拥有的训练数据多,就能在未知数据的附近发现训练数据”这一假设。这个假设叫作渐近假设,但对于高维数据来说,这个假设不一定成立。