这篇文章上次修改于 234 天前,可能其部分内容已经发生变化,如有疑问可询问作者。
算法一:线性回归
概述
线性回归很常见,简单带过,就是把xy对应数据拟合成线性关系。
对于直线方程,有 ,其中有两个参数也就是k和b分别是斜率和截距。
- 学习参数:算法学得的参数例如斜率k和截距b。
- 一元回归:指的是只有一个特征变量的情况,即模型只使用一个自变量去预测目标变量。
算法说明
线性回归中,需要从不在一条直线上的点求出直线。为了判断学习参数的优劣性,使用均方误差进行判断。
均方误差:每个目标变量与直线的差值平方和
均方误差越小,越能更好的表示数据关联性。
- 误差函数:能表明学习参数和误差之间的关系的函数,例如此处的均方误差。
线性回归代码演示
from sklearn.linear_model import LinearRegression
import matplotlib.pyplot as plt
import numpy as np
from sklearn.model_selection import train_test_split
X = [[10.0], [8.0], [13.0], [9.0], [11.0], [14.0], [6.0], [4.0], [12.0], [7.0], [5.0]]
y = [8.04, 6.95, 7.58, 8.81, 8.33, 9.96, 7.24, 4.26, 10.84, 4.82, 5.68]
# 划分训练集和测试集,test_size 指定测试集的比例
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
model = LinearRegression()
model.fit(X_train, y_train)
print(model.intercept_) # 截距
print(model.coef_) # 斜率
y_pred = model.predict([[0], [1]])
print(y_pred) # 对x=0, x=1的预测结果
# 绘制数据集散点图
plt.scatter(X_train, y_train, color='blue', label='Data')
# 绘制回归线
y_pred = model.predict(X_train)
plt.plot(X_train, y_pred, color='red', label='Linear Regression Model')
plt.show()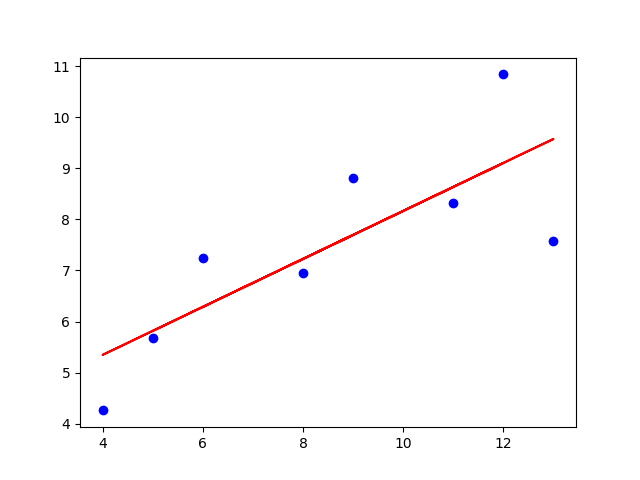
详细说明
安斯库姆四重奏
安斯库姆四重奏(Anscombe’s Quartet)是一组由统计学家弗朗西斯·安斯库姆(Francis Anscombe)在 1973 年提出的数据集。它由四组不同的数据构成,尽管这些数据在许多统计属性上(如均值、方差、相关系数、线性回归直线等)非常相似,但它们的分布形态却大不相同。
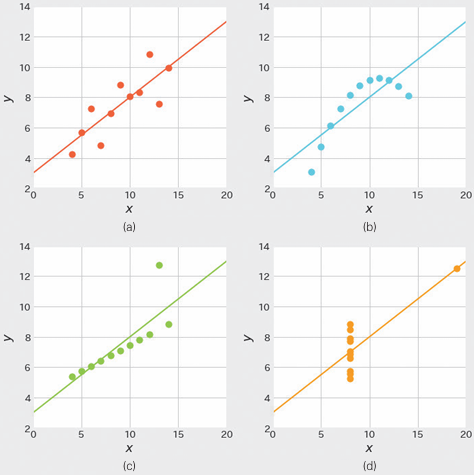
以上的四组数据线性回归直线完全一致,但我们明显可以发现有部分的数据并不适合这样拟合。
对原本不遵循线性分布的数据强行进行线性回归也得不到好的结果。拿到数据之后,首先应该进行可视化,再考虑是否进行线性回归。
最小化均方误差
均方误差可以使用学习参数的函数表示:
此时代入xi yi,这里使用以下值作为例子
| i | x | y |
|---|---|---|
| 1 | 2 | 1 |
| 2 | 3 | 5 |
| 3 | 6 | 3 |
| 4 | 7 | 7 |
可以得到以下 由此二次函数可得图像(w0=b,w1=k):
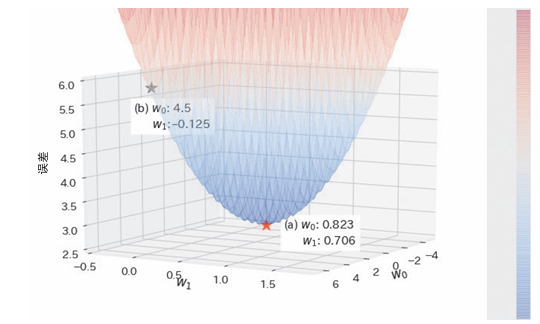
可以发现a点是最佳学习参数
其它线性回归和非线性回归
- 一元回归:指独立特征变量只有一个时的线性回归。
- 多元回归:当特征变量有两个及以上时,称作多元回归。
- 多项式回归:包含特征变量的多次方项的线性回归。
- 非线性回归:例如e的kx次,学习参数和目标变量不是线性关系,被分为非线性回归。
是否为线性回归不是从特征变量来看的。从学习参数的角度来看是线性的回归才称为线性回归,所以多项式回归也属于线性回归。
算法二:正则化
概述
正则化是防止过拟合的一种方法,与线性回归等算法配合使用。通过向损失函数增加惩罚项的方式对模型施加制约,有望提高模型的泛化能力。
- 过拟合:模型在验证数据上的误差比训练数据的误差大得多的现象
- 泛化程度:机器学习模型在新数据上的表现能力,具体来说是模型能否在训练集之外的数据上取得良好的性能。
(其中的一个原因:模型复杂度过高)
对于以下例子,数据是y = sin(2pi x),使用多次进行线性回归。
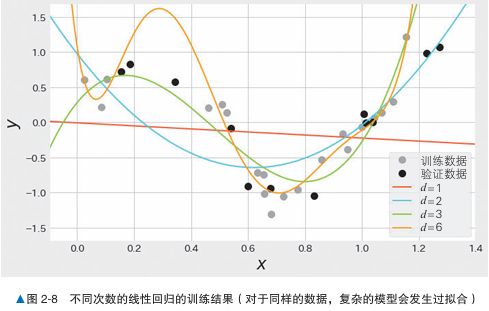
| 次数 | x | y |
|---|---|---|
| 1 | 0.412 | 0.618 |
| 2 | 0.176 | 0.193 |
| 3 | 0.081 | 0.492 |
| … | … | … |
| 6 | 0.024 | 3.472 |
我们可以发现第六次线性回归的误差值是最小的,但是验证误差十分大,这就是一个过拟合的例子,六次线性回归的模型太过复杂,由于过拟合导致泛化程度低。
应用正则化后就会抑制模型复杂度,防止后期的过拟合。
算法说明
岭回归(Ridge Regression)是一种线性回归的改进方法,常用于解决多重共线性问题(即解释变量之间高度相关)和防止模型过拟合。
之所以复杂模型会出现过拟合:学习参数值太大或太小。
随着学习此处的增加,学习参数的绝对值会变大,但使用了正则化则会减少这种情况。
岭回归的误差函数
考虑对二次线性回归应用正则化的情况:
第1项 是线性回归的损失函数。
第2项 被称为惩罚项(或者正则化项),是学习参数的平方和的形式。
一般来说,惩罚项中不包含截距。
α控制了正则化强度,α越大,对学习参数的抑制就越强。
损失函数最小化
岭回归的误差函数就是在后面加上了惩罚项,距我们之前所说,造成过拟合的原因是w值的绝对值过大,因此如果w值的绝对值过大,就增加惩罚项,从而避免过拟合。
用于抑制学习参数。
示例代码
对sin函数进行岭回归建模
import numpy as np
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import Ridge
from sklearn.metrics import mean_squared_error
train_size = 20
test_size = 12
train_X = np.random.uniform(low=0, high=1.2, size=train_size)
test_X = np.random.uniform(low=0.1, high=1.3, size=test_size)
train_y = np.sin(train_X * 2 * np.pi) + np.random.normal(0, 0.2, train_size)
test_y = np.sin(test_X * 2 * np.pi) + np.random.normal(0, 0.2, test_size)
poly = PolynomialFeatures(6) # 次数为6
train_poly_X = poly.fit_transform(train_X.reshape(train_size, 1))
test_poly_X = poly.fit_transform(test_X.reshape(test_size, 1))
model = Ridge(alpha=1.0)
model.fit(train_poly_X, train_y)
train_pred_y = model.predict(train_poly_X)
test_pred_y = model.predict(test_poly_X)
print(mean_squared_error(train_pred_y, train_y))
print(mean_squared_error(test_pred_y, test_y))
# 0.2525090370132518
# 0.34030978733484846详细说明
控制α来调整正则化强度,应一边验证误差一边对α进行调整,最终得到合适的α。
Lasso回归
Lasso 回归的惩罚项是学习参数的绝对值之和,这一点与岭回归不同。
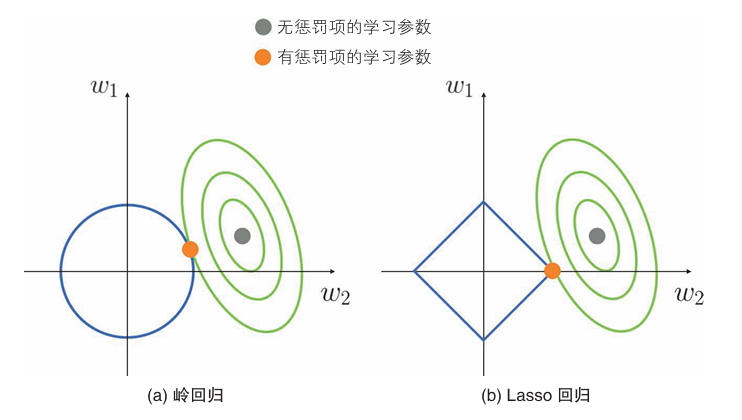
绿色是误差函数,蓝色是惩罚项。
如Lasso 回归所示,具有学习参数容易变为0的特点。利用这个特点,我们可以使用学习参数不为0的特征来构建模型,从而达到利用Lasso回归选择特征的效果。这样不仅能提高模型的泛化能力,还能使模型的解释变容易。
算法三:逻辑回归
概述
逻辑回归是一种用于有监督学习的分类任务的简单算法。逻辑回归通过计算数据属于各类别的概率来进行分类。利用这个概率,可以对某个事件发生或不发生进行二元分类(也可以三元以上分类)
这次的例子是,给定100天里,温度对应是否有积雪的情况,y轴为0时有积雪,为1无积雪。
x轴是摄氏度气温,可以看到高温没积雪,低温有积雪。
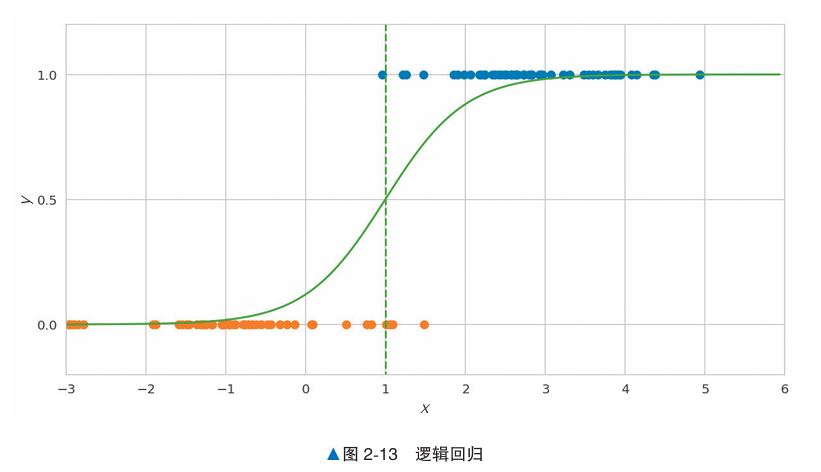
上图是对数据的逻辑回归,在0度的时候是12%,1度50%,2度88%。
算法说明
逻辑回归根据数据x和表示其所属类别的标签y进行学习,计算概率。
如果标签是二元分类,则可以使用前面的y=0, 1这种二元数值表示。
与线性回归进行比较:
相同点:基本思想,对数据x乘以权重向量w,再加上偏置w0,计算wT x+w0的值
不同点:逻辑回归的输出范围限制在01之间,使用了Sigmoid函数:
σ(z)=1/[1+exp(-z)]
对输入数据x使用Sigmoid函数,p=σ(wT x+w0) 得到标签为y的概率p。(二元分类使用0.5作为阈值)
误差函数使用逻辑损失。逻辑损失在分类失败时返回大值,在分类成功时为小值。
与在误差回归中引入的均方误差不同的是,我们无法通过式子变形来计算逻辑损失的最小值,因此需要采用梯度下降法通过数值计算来求解。(机器学习中经常会通过数值计算来近似求解)
示例代码
以下代码就是对之前温度和积雪预测的实例,最后输出了各种概率。
import numpy as np
from sklearn.linear_model import LogisticRegression
X_train = np.r_[np.random.normal(3, 1, size=50),
np.random.normal(-1, 1, size=50)].reshape((100, -1))
y_train = np.r_[np.ones(50), np.zeros(50)]
model = LogisticRegression()
model.fit(X_train, y_train)
model.predict_proba([[0], [1], [2]])[:, 1]
# array([ 0.12082515, 0.50296844, 0.88167486])详细说明
- 决策边界:逻辑回归计算出来概率正好为50%的位置
决策边界的形状因使用的算法不同而有很大的不同。在平面的情况下,逻辑回归的决策边界是直线。其它算法的决策边界会更复杂
特征
如何通过逻辑回归模型中的特征权重(系数)来理解每个特征对分类结果的影响。
在逻辑回归中,每个特征(比如鸢尾花的花瓣长、花瓣宽等)都有一个权重值。权重的符号(正或负)和大小告诉我们该特征对分类结果的影响:
- 正的权重:如果这个特征值增加,模型认为该数据属于目标类别的概率(这里是杂色鸢尾)就越大。
- 负的权重:如果这个特征值增加,模型认为该数据属于目标类别的概率反而会降低。
举个例子,这里用的是鸢尾花的数据,分类目标是预测一朵花是“杂色鸢尾”(versicolor)还是“山鸢尾”(setosa)。两个特征“花瓣长度”(petal length)和“萼片宽度”(sepal width)分别有正的和负的权重:
- 花瓣长度的权重是正的,表示如果花瓣长度越长,模型就越倾向于把这朵花分类为杂色鸢尾。
- 萼片宽度的权重是负的,表示如果萼片宽度越小,模型就越倾向于把这朵花分类为杂色鸢尾。
这样,通过查看权重的符号和大小,我们能直观地理解每个特征对分类结果的影响方向和程度。