《图解机器学习算法》笔记——评估方法和各种数据的处理 2024.11.29 机器学习

有监督学习的评估

现梳理有监督学习的常见的评估方法、提高机器学习性能的方法，以及提高性能时的障碍。

分类问题的评估

混淆矩阵

混淆矩阵可以将分类结果以表格的形式汇总，这样就可以检查哪些标签分类正确，哪些标签分类错误。

混淆矩阵是一个评估工具，而并不是一个评估指标，通过使用混淆矩阵，我们可以再通过指标进行评估。

构成

混淆矩阵是一个二维矩阵，用于展示模型预测结果与真实标签之间的对比。对于二分类问题，矩阵的结构通常如下：

	预测为正类	预测为负类
实际为正类	True Positives (TP)	False Negatives (FN)
实际为负类	False Positives (FP)	True Negatives (TN)

• True Positives (TP): 被正确分类为正类的样本数。
• True Negatives (TN): 被正确分类为负类的样本数。
• False Positives (FP): 被错误分类为正类的负类样本数。
• False Negatives (FN): 被错误分类为负类的正类样本数。

实例说明

通过代码，我们得到一个数据来进行更为具体的说明

from sklearn.metrics import confusion_matrix
cm = confusion_matrix(y, y_pred)
print(cm)
"""
[[341   16]
[ 36  176]]
"""

通过上例子，TN有341条，TP有176条，FN有36条，FP有16条。

由于使用的数据是肿瘤预测，因此进行更具体的例子解释：

• 有36个恶性肿瘤患者被漏诊
• 有16个良性肿瘤患者被误诊
• 有341个恶性肿瘤正确诊断
• 有176个良性肿瘤正确诊断

四个指标公式

• 正确率 (Accuracy)：
• 精确率 (Precision)：
• 召回率 (Recall)：
• F值 (F1 Score)：

对于以上的四个指标，以下分别说明并解释使用环境。

正确率

正确率表示所有预测中正确预测的比例。使用accuracy_score函数：

from sklearn.metrics import accuracy_score
accuracy_score(y, y_pred)
#  0.908611599297012

精确率

精确率表示被预测为正类的样本中，实际为正类的比例。

具体来说，精确率指的是在所有被预测为阳性的数据中，被正确预测为阳性的数据所占的比例。使用precision_score函数：

from sklearn.metrics import precision_score
precision_score(y, y_pred)
#  0.9166666666666666

精确率低，意味着预测为恶性的病例之中包含了其实是良性的病例。在这种情况下，可以通过再次检查等方式解决精确率低的问题

召回率

召回率表示实际为正类的样本中，被正确预测为正类的比例。

也就是召回率指的是在实际为阳性的数据中，被正确预测为阳性的数据所占的比例。使用recall_score函数：

from sklearn.metrics import recall_score
recall_score(y, y_pred)
#  0.8301886792452831

在这个问题中，它表示实际为恶性中被正确预测所占的比例。

召回率低，意味着实际为恶性的病例大部分被预测为良性。与精确率低的情况相比，召回率低的问题更严重。

在使用这样的模型解决实际问题之前，需要想办法提高召回率。

F值

F1 分数是精确率和召回率的调和平均数，用来综合考虑两者的表现。f1_score函数用于计算F值：

from sklearn.metrics import f1_score
f1_score(y, y_pred)
# 0.8712871287128713

精确率和召回率之间是此消彼长的关系，如果试图让其中一个的值更高，则会导致另一个的值更低。如果这两个指标同等重要，可以观察F值。

预测概率

在进行二元分类时，预测结果必须为0或者1这两个值中的一个。但实际情况下，大多数模型得到的都是两个预测结果的分别概率。

同时 predict 函数将概率阈值设置成50%。

如果要查看的是分别概率，可以使用predict_proba函数方法：

model_lor.predict_proba(X)
"""
array([[4.41813058e-03, 9.95581869e-01],
       [4.87318118e-04, 9.99512682e-01],
       [3.31064277e-04, 9.99668936e-01],
       ...,
       [2.62819353e-02, 9.73718065e-01],
       [5.09374706e-06, 9.99994906e-01],
       [9.74068776e-01, 2.59312242e-02]]
"""

根据概率，我们可以自行调整阈值，例如我们宁愿错诊，不愿漏诊，我们可以这个阈值降低为第二项的概率超过10%

import numpy as np
y_pred2 = (model_lor.predict_proba(X)[:, 1]>0.1).astype(np.int)
print(confusion_matrix(y, y_pred2))
"""
[[259  98]
 [  2 210]]
"""

此时的混淆矩阵就明显减少了漏诊的情况。

正确率下降到0.82左右，但是召回率非常高，达到了0.99左右。

ROC曲线与AUC

对于数据数据有偏差的时候，例如阳性的数据有95个，阴性的数据只有5个，此时的预测正确率等就会出现一些偏差，让像傻子一样只说阳性的模型也能有很高正确率。

应对数据不均衡问题的指标有AUC （Area Under the Curve，曲线下面积）。

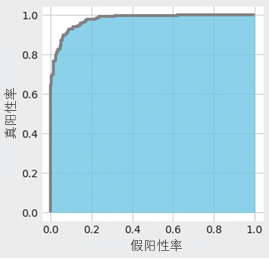
ROC曲线

这里的ROC曲线的是横轴为假阳性率（即FP的占比），纵轴为真阳性率（即TP的占比）的图形。图中显示了当预测数据为阳性的预测概率的阈值从1开始逐渐下降时，FP和TP之间关系的变化。

示例代码

roc_curve函数的输入是目标变量（类别标签数据）和预测概率。这里使用predict_proba方法计算了预测概率。下面在Matplotlib中对roc_curve函数输出的fpr和tpr进行可视化。

import matplotlib.pyplot as plt
from sklearn.metrics import roc_curve

probas = model_lor.predict_proba(X)
fpr, tpr, thresholds = roc_curve(y, probas[:, 1])
# roc_curve 计算ROC曲线

plt.style.use('fivethirtyeight')
fig, ax = plt.subplots()
fig.set_size_inches(4.8, 5)
ax.step(fpr, tpr, 'gray')
ax.fill_between(fpr, tpr, 0, color='skyblue', alpha=0.8)
ax.set_xlabel('False Positive Rate')
ax.set_ylabel('True Positive Rate')
ax.set_facecolor('xkcd:white')
plt.show()

AUC

应对数据不均衡问题的指标有AUC （Area Under the Curve，曲线下面积）。AUC指的是ROC（Receiver Operating Characteristic，接收器操作特性）曲线下的面积。

ROC曲线下方的面积是AUC。面积的最大值是1，最小值是0。AUC越接近于1（面积越大），说明精度越高；如果其值在0.5左右，则说明预测不够理想。换言之，如果值在0.5左右，则得到的分类模型和抛硬币随机决定良性恶性没多大区别。

from sklearn.metrics import roc_auc_score
roc_auc_score(y, probas[:, 1])
# 0.9767322023148881

这个AUC的结果代表模型精度很高。

在处理不均衡数据时，我们使用AUC作为指标

回归问题的评估方法

先给出一个例子，在实例下进行以下评估方法的说明：

from sklearn.datasets import load_boston
data = load_boston()
X = data.data[:, [5,]]
y = data.target

这里使用的是美国波士顿的房价数据集。这个数据集有 13 个特征变量，目标变量是5.0 ～ 50.0的数值。简单起见，这里介绍一元回归的评估方法，所以我们只使用13个特征变量中的“住宅平均房间数”

from sklearn.linear_model import LinearRegression
model_lir = LinearRegression()
model_lir.fit(X, y)
y_pred = model_lir.predict(X)
print(model_lir.coef_)  # 斜率k
print(model_lir.intercept_)  # 截距b
"""
array([9.10210898])
-34.67062077643857
"""

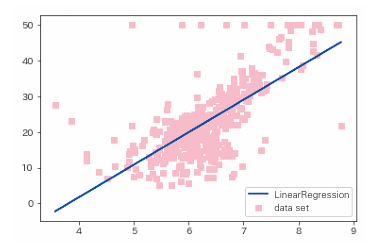
以上是预测结果的可视化。

均方误差

平方误差是一个表示实际值和预测值之间存在多大差异的数值。

取每个实际值和预测值之间的差的平方和的平均值就是均方误差。

mean_squared_error函数可以得到均方误差

from sklearn.metrics import mean_squared_error
mean_squared_error(y, y_pred)
#  43.60055177116956

决定系数（R2）

R2是使用均方误差来表示训练好的模型的预测效果的数值。

当该系数取最大值1.0时，说明没有误差，越接近1.0，说明模型对数据点的解释能力越强。

它的值通常在0.0和1.0之间，但如果预测的误差过大，也可能为负值。

我们可以使用r2_score函数计算决定系数

from sklearn.metrics import r2_score
r2_score(y, y_pred)
#  0.48352545599133423

如果目标变量的方差较大，均方误差也会变大，故光看均方误差的数值不能判断精度是好还是坏。

而决定系数使用不依赖于目标变量方差，取值范围在0.0和1.0之间，即使目标变量的数量级不同，也可以将决定系数作为一般的指标使用。

与其他算法比较

下面使用其他算法与LinearRegression比较

SVR

SVR是将第二章的支持向量机应用于回归得到的算法。

from sklearn.svm import SVR
model_svr_linear = SVR(C=0.01, kernel='linear')
model_svr_linear.fit(X, y)
y_svr_pred = model_svr_linear.predict(X)
# 导入了SVR类，下面对比两种算法
%matplotlib inline
import matplotlib.pyplot as plt
fig, ax = plt.subplots()
ax.scatter(X, y, color='pink', marker='s', label='data set')
ax.plot(X, y_pred, color='blue', label='LinearRegression')
ax.plot(X, y_svr_pred, color='red', label='SVR')
ax.legend()
plt.show()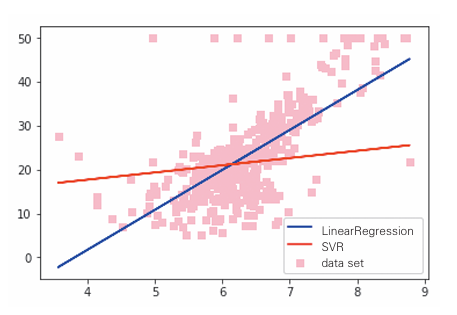

print(mean_squared_error(y, y_svr_pred))  # 均方误差
print(r2_score(y, y_svr_pred))  # 决定系数
print(model_svr_linear.coef_)  # 斜率
print(model_svr_linear.intercept_)  # 截距
#72.14197118147209
#0.14543531775956597
#[[1.64398]]
#11.13520958

与线性回归相比，SVR的均方误差和决定系数都相对较差。

通过改变SVR的C和kernel参数可以改善SVR的均方误差和决定系数。

超参数的设置

将C改为1.0，kernal改为‘rbf’。

model_svr_rbf = SVR(C=1.0, kernel='rbf')
model_svr_rbf.fit(X, y)
y_svr_pred = model_svr_rbf.predict(X)
print(mean_squared_error(y, y_svr_pred))  # 均方误差
print(r2_score(y, y_svr_pred))  # 决定系数
#36.42126375260171
#0.5685684051071418

超参数是在训练前由用户给出的，若设置得不好，模型的性能就可能会很差。

模型的过拟合

以下代码将数据集分为训练数据和用来确认性能的验证数据，如何进行SVR 的训练和预测。

train_X, test_X = X[:400], X[400:]
train_y, test_y = y[:400], y[400:]
model_svr_rbf_1 = SVR(C=1.0, kernel='rbf')
model_svr_rbf_1.fit(train_X, train_y)
test_y_pred = model_svr_rbf_1.predict(test_X)
print(mean_squared_error(test_y, test_y_pred))  # 均方误差
print(r2_score(test_y, test_y_pred))  # 决定系数
#69.16928620453004
#-1.4478345530124388

这种对训练数据的预测效果好，但对验证数据（没用于训练的数据）的预测效果不好的现象叫做过拟合。

模型对未知数据的预测能力叫做泛化能力。在解决实际问题时，这种能力非常重要。如果发生过拟合，泛化能力也会很低。

防止过拟合的方法

以乳腺癌数据集为例，“患者的身体数据”（特征）和“恶性/良性”（目标变量）是训练数据。实际应用中，对于“恶性/良性”不明的患者，重要的是能否通过患者的体检数据预测出“恶性/良性”。

以下是一些代表性的方法

将数据分为训练数据和验证数据

即不使用所有的数据进行训练，留出一部分用于验证。

使用scikit-learn 的 train_test_split 函数来分割函数。

from sklearn.datasets import load_breast_cancer
data = load_breast_cancer()
X = data.data
y = data.target
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3)

• 训练用的特征值：X_train
• 验证用的特征值：X_test
• 训练用的目标变量：y_train
• 验证用的目标变量：y_test

分割比例没有明确规定，如果数据集很大，可以设置为6：4，如果太小，则可以设置为8：2.以上代码分割为7：3。下面是结果。

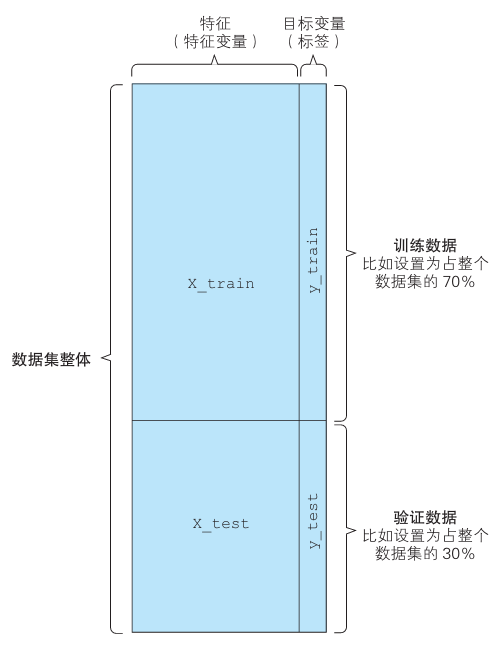
下面使用训练数据和验证数据来进行算法的学习，并创建模型。

from sklearn.svm import SVC
 model_svc = SVC()
 model_svc.fit(X_train, y_train)
 y_train_pred = model_svc.predict(X_train)
 y_test_pred = model_svc.predict(X_test)
 from sklearn.metrics import accuracy_score
 print(accuracy_score(y_train, y_train_pred))
 print(accuracy_score(y_test, y_test_pred))
#1.0
#0.6023391812865497

如果验证数据的正确率比训练数据低很多，说明数据发生了过拟合。上述代码对未知数据的正确率约为60%。

下面使用RandomForestClassifier试一下。

from sklearn.ensemble import RandomForestClassifier
model_rfc = RandomForestClassifier()
model_rfc.fit(X_train, y_train)
y_train_pred = model_rfc.predict(X_train)
y_test_pred = model_rfc.predict(X_test)
from sklearn.metrics import accuracy_score
print(accuracy_score(y_train, y_train_pred))
print(accuracy_score(y_test, y_test_pred))
# 0.9974874371859297
# 0.9590643274853801

这次对验证数据的正确率约为96%，可以说防止了过拟合。

光从模型对训练数据的正确率来看，我们可能会选择SVC，但通过观察验证数据的正确率，我们会选择RandomForestClassifier。

交叉验证

如果训练数据和验证数据碰巧非常相似（或者非常不相似），则上述办法仍可能发生过拟合。为了避免这种误差，可使用不同分割方案进行多次验证，称为交叉验证。

我们将数据分割5次以作例子。

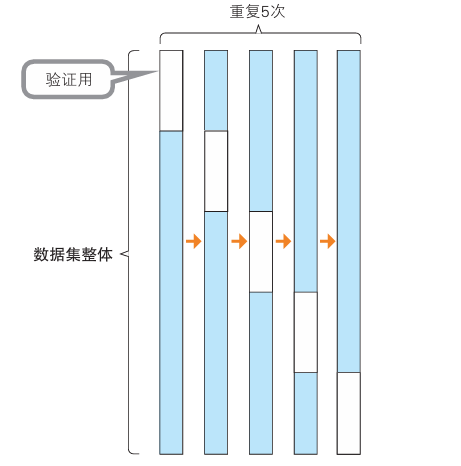
在这个例子中，验证数据按分组顺序分别分割，但在实际应用中，验证数据是随机抽取的。

示例代码

from sklearn.model_selection import cross_val_score
from sklearn.model_selection import KFold
cv = KFold(5, shuffle=True)
model_rfc_1 = RandomForestClassifier()
cross_val_score(model_rfc_1, X, y, cv=cv, scoring='accuracy')
# array([0.99122807, 0.92982456, 0.94736842, 0.96491228, 0.92920354])

我们看到五个正确率有高有低，在选择模型时，需要考虑所有正确率的均值和方差。

另外还可以输出F值的评估结果。

• 通过将cross_val_score函数的scoring参数定义为f1，就可以输出F值。

cross_val_score(model_rfc_1, X, y, cv=cv, scoring="f1")
# array([0.99280576, 0.93846154, 0.97902098, 0.97297297, 0.97435897])

防止过拟合的其他方法

• 增加训练数据
• 减少特征值
• 正则化
• Early Stopping
• 集成学习

搜索超参数

在不会发生过拟合的基础上，仔细地选择超参数，就可以进一步提高模型的性能。

以下介绍搜索超参数的方法。

使用网格搜索选择超参数

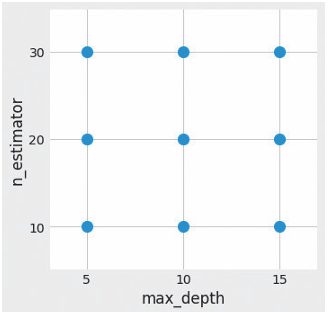
网格搜索是一种自动搜索超参数的方法。其对各个超参数（事先确定的超参数）组合进行穷尽搜索。

示例代码

下面是使用scikit-learn的 GridSearchCV进行RandomForestClassifier超参数搜索的示例代码。 GridSearchCV一边关注对验证数据的性能，一边执行超参数的搜索。

from sklearn.datasets import load_breast_cancer
data = load_breast_cancer()
X = data.data
y = 1 - data.target
# 反转标签的0和1
X = X[:, :10]
# 以上加载了美国威斯康星州乳腺癌数据集

from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import GridSearchCV
from sklearn.model_selection import KFold
cv = KFold(5, shuffle=True)
param_grid = {'max_depth': [5, 10, 15], 'n_estimators': [10, 20, 30]}
model_rfc_2 = RandomForestClassifier()
grid_search = GridSearchCV(model_rfc_2, param_grid, cv=cv, scoring='accuracy')
grid_search.fit(X, y)
#网格搜索

print(grid_search.best_score_)
print(grid_search.best_params_)
# 0.9490333919156415
#{'max_depth': 10, 'n_estimators': 10}

除了交叉验证，网格搜索还支持使用F值进行评估。即将scoring参数指定为f1。

grid_search = GridSearchCV(model_rfc_2, param_grid, cv=cv, scoring='f1')

文本数据的转换处理

对于自然语言处理，要对文本数据进行一定的处理。

基于单词出现次数的转换

对每个文本的每个单词进行计数。

建立一个表格，每一列表示一个单词，每一行表示一个文本。

对于一个单元格来说，代表的是这个文本中单词出现的个数。

以上方法是只考虑单词的出现次数，所有的单词并没有权重

基于tf-idf 的转换

• tf（term frequency，词频）：在文本中出现的频率
• idf（inverse document frequency，逆文本频率指数）：是一个包含该单词的文本越多，值就越小的值
• tf-idf：这两个指标相乘得到的结果

例如对于

文本1：“This is my car” 文本2：“This is my friend” 文本3：“This is my English book“

频率表：

	This	is	my	car	friend	English	book
文本 1	1	1	1	1	0	0	0
文本 2	1	1	1	0	1	0	0
文本 3	1	1	1	0	0	1	1

tf-idf转换后：

	This	is	my	car	friend	English	book
文本 1	0.41	0.41	0.41	0.70	0.00	0.00	0.00
文本 2	0.41	0.41	0.41	0.00	0.70	0.00	0.00
文本 3	0.34	0.34	0.34	0.00	0.00	0.57	0.57

行业术语和专有名词等只在特定文本中出现的词，往往具有较大的tf-idf值，有时能够很好地表示包含这些单词的文本。This 和 my等单词在每个文本中都出现了，所以它们的tf-idf值较小。

应用于机器学习模型

应用于机器学习模型

下面基于单词出现次数和 tf-idf 将文本数据转换为表格形式的特征数据，并应用于机器学习模型。

scikit-learn 的 CountVectorizer 可以计算单词出现次数，TfidfVectorizer 可以进行 tf-idf 的转换。

另外，通过 fetch_20newsgroups 获取使用的文本数据，机器学习模型则采用 LinearSVC。

示例代码

import numpy as np
from sklearn.feature_extraction.text import CountVectorizer, TfidfVectorizer
from sklearn.svm import LinearSVC
from sklearn.datasets import fetch_20newsgroups

categories = ['misc.forsale', 'rec.autos', 'comp.graphics', 'sci.med']
remove = ('headers', 'footers', 'quotes')
twenty_train = fetch_20newsgroups(subset='train',
                                  remove=remove,
                                  categories=categories)  # 训练数据
twenty_test = fetch_20newsgroups(subset='test',
                                 remove=remove,
                                 categories=categories)  # 验证数据

这里使用的是前面出现过的 20 Newsgroups 数据集，代码通过 categories 变量明确指定了 4 个主题的数据。

首先将文本数据转换为单词出现次数，然后使用 LinearSVC 学习和预测。得到的模型对验证数据的正确率约为 0.794。也就是说，我们成功地将文本数据转换为了表格形式的特征，并进行了机器学习。

示例代码

count_vect = CountVectorizer()  # 单词出现次数
X_train_counts = count_vect.fit_transform(twenty_train.data)
X_test_counts = count_vect.transform(twenty_test.data)

model = LinearSVC()
model.fit(X_train_counts, twenty_train.target)
predicted = model.predict(X_test_counts)
np.mean(predicted == twenty_test.target)
#  0.7937619350732018

接下来使用tf-idf进行转换，然后以同样的方式进行训练和预测。此时得到的模型的正确率约为0.87，比基于单词出现次数进行转换的方法的正确率高。通过tf-idf，看起来我们很好地抓住了文本数据的特点。

tf_vec = TfidfVectorizer()  # tf-idf
X_train_tfidf = tf_vec.fit_transform(twenty_train.data)
X_test_tfidf = tf_vec.transform(twenty_test.data)
model = LinearSVC()
model.fit(X_train_tfidf, twenty_train.target)
predicted = model.predict(X_test_tfidf)
np.mean(predicted == twenty_test.target)
# 0.8701464035646085

图像数据的转换处理

本节将说明如何将图像数据作为机器学习的输入数据。

直接将像素信息作为数值使用

• 灰度图像：是图像中的每个像素只表示亮度的图像

以灰度图形作为例子，以下是将图像数据转换为向量数据的例子。如果是简单的图像识别问题，就可以使用这种简单的转换建立一个具有一定精度的模型。

转换为一维的数据

将灰度按照顺序记录，得到的向量就是图片数据

这种转化丢失了二维的图像关系，失去了输入图像的重要信息

转化为二维的数据

有些模型会在保留图像的二维关系的前提下直接将其作为输入数据进行处理，比如在图像识别中常用的深度学习使用的就是像素的近邻像素的信息。 下面是将图像数据转换为向量数据的示例代码。代码中使用第三方Python包Pillow将图像（png）数据转换为了向量数据。

from PIL import Image
import numpy as np
img = Image.open('mlzukan-img.png').convert('L')
width, height = img.size
img_pixels = []
for y in range(height):
    for x in range(width):
        # 通过getpixel获取指定位置的像素值
	      img_pixels.append(img.getpixel((x,y)))
print(img_pixels)

数据使用

以下是一个图像转化为向量数据后输入给机器学习模型的例子：

这里我们使用灰度手写数字数据建立一个模型，用于预测从0到9的10个数字。

from sklearn import datasets
from sklearn import metrics
from sklearn.ensemble import RandomForestClassifier
digits = datasets.load_digits()
n_samples = len(digits.images)
data = digits.images.reshape((n_samples, -1))
model = RandomForestClassifier()
model.fit(data[:n_samples // 2], digits.target[:n_samples // 2])
expected = digits.target[n_samples // 2:]
predicted = model.predict(data[n_samples // 2:])
print(metrics.classification_report(expected, predicted))

从预测结果来看，使用了向量数据的模型成功地进行了高精度的预测。