算法五：k-means算法

概述

  • 聚类：把相似的数据汇总为簇的方法

该算法是一种聚类算法。

输入是多个数据点，并设置要聚类的簇数量，例如以下：

1.png

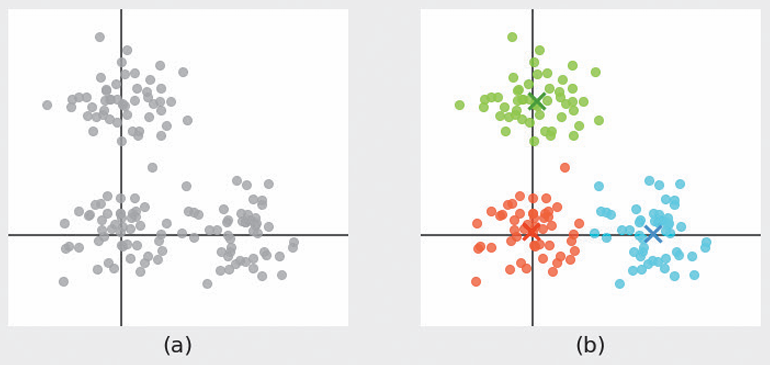
给定图a的数据点，要求分成3簇，图中给出了三个X，代表了三个簇的中心。求簇的重心就是聚类算法的重要计算。

算法说明

2.png

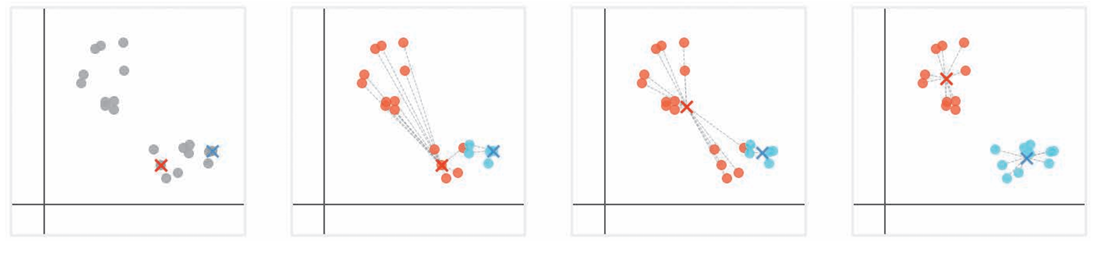
如上图重复步骤：

  • 从数据点中随机选择和簇数量相同的点，作为簇的重心
  • 计算每个数据点到各重心之间的距离，将自己归类为最近的簇重心的簇
  • 计算每个簇的数据点的平均值，作为新的重心。
  • 重复步骤2和步骤3.知道所有数据点不改变所属的簇。

注：

有时选择的重心不好可能会导致步骤2和步骤3的训练无法顺利进行。

在随机选择的重心之间太近等的情况下，就会出现这种问题。

利用k-means++等方法，选择位置尽可能远离的数据点作为重心的初始值，就可以解决这个问题。

示例代码

下面是对鸢尾花数据集应用k-means算法的代码。

from sklearn.cluster import KMeans
from sklearn.datasets import load_iris
data = load_iris()
n_clusters = 3  # 将簇的数量设置为3
model = KMeans(n_clusters=n_clusters)
model.fit(data.data)
print(model.labels_)  # 各数据点所属的簇
print(model.cluster_centers_)  # 通过fit()计算得到的重心

详细说明

k-means的评估

用于评估分类的结果好坏，可以使用WCSS（簇内平方和）。也就是每个簇内的所有数据到重心距离的平方和相加的值。

WCSS越小，说明聚类结果越好。

Elbow方法确定簇数量

对于簇数量，是作为输入的超参数，也就是我们算法名称中的k，有些数据集很难定义合适的簇数量。

我们已经知道可以使用WCSS来确定优劣，因此对于不同的簇数量，我们都可以得到一个WCSS。

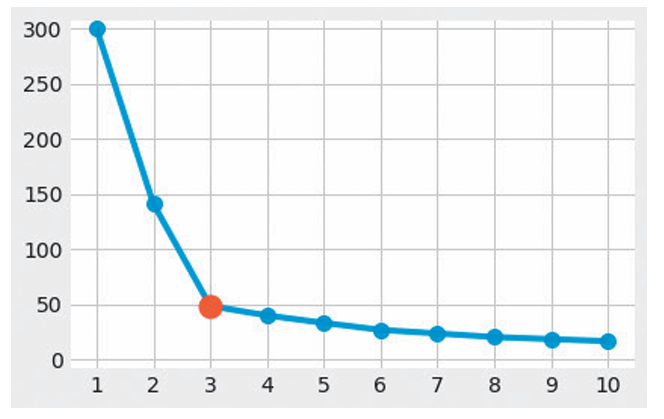
image.png

纵轴是WCSS，横轴是k，可以发现，随着k的变大，WCSS会递减，但是我们可以找到一个点 3，在这个点后，WCSS的变化值显著减少，也就是选择这个点是最适合的点，这个图像类似于一个肘部，因此称作肘方法。

注：

当没有很明确的理由来确定簇的数量或对数据知之甚少时，Elbow方法很有用。不过在实际的分析中，常常不会出现图中那样明显的“肘部”，所以Elbow方法的结果只不过是一种参考而已。

算法六：混合高斯分布

概述

如果数据集中有多组数据，可以使用混合高斯分布（即多个高斯分布的线性组合）来实现聚类。

高斯分布是一种概率分布的名称，使用概率分布产生的数据估计分布参数的方法。

高斯分布认为数据的分布可以用均值和方差表示（正态分布）

  • 均值：是数据的中心位置
  • 方差：是数据的离散程度

混合高斯分布是以多个高斯分布的线性叠加表示数据的模型。

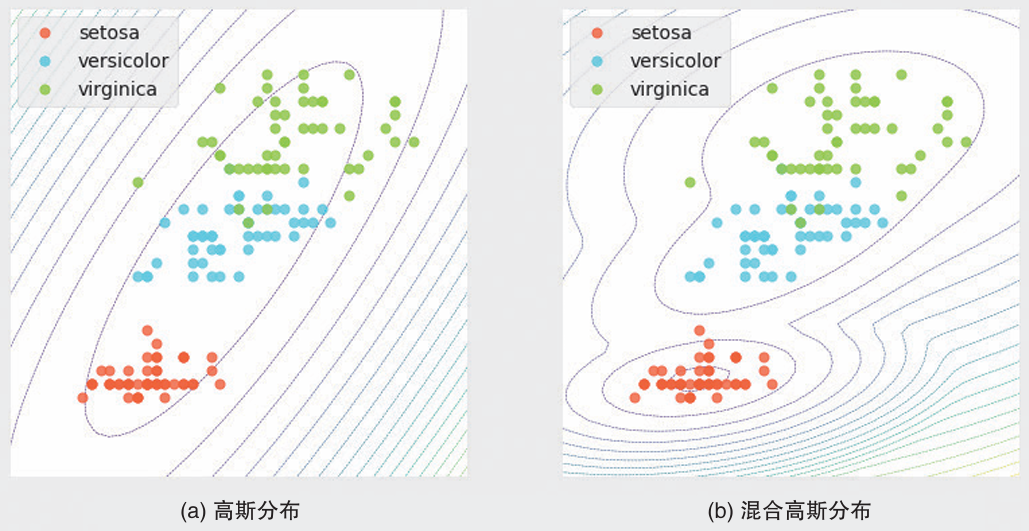
image.png

以上是对鸢尾花数据使用高斯分布和混合高斯分布的结果。

对于高斯分布，每个轴只有一个均值和一个方差，所以使用一个分布无法提现不同品种的差异。

对于混合高斯分布，使用了三个高斯分布叠加而成，可以表示多个类别组成的复杂数据。

算法说明

混合高斯分布的学习过程是从输入数据中找到每个高斯分布的均值和方差。

对于一个已经了解的高斯分布，做一维数据进行示例：

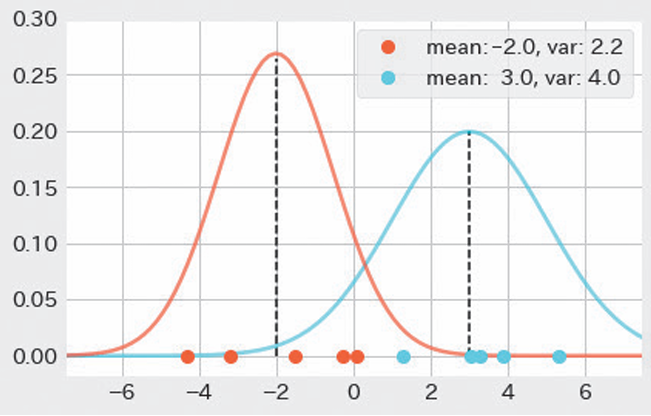
image.png

这个一维数据由两个高斯分布分类。

但实际上，混合高斯分布必须在不知道每个数据点的类别的情况下求出参数。

因此，我们需要在推测“每个数据点属于某个类别”的权重的基础上，计算出数据点的各个类别的高斯分布的参数（均值和方差）。

步骤：

  • 初始化参数（各高斯分布的均值和方差）
  • 对每个类别计算数据点的权重
  • 根据步骤2 中计算出的权重重新计算参数
  • 重复 步骤2 步骤3 ，知道步骤3更新前后的每个均值的变化够小

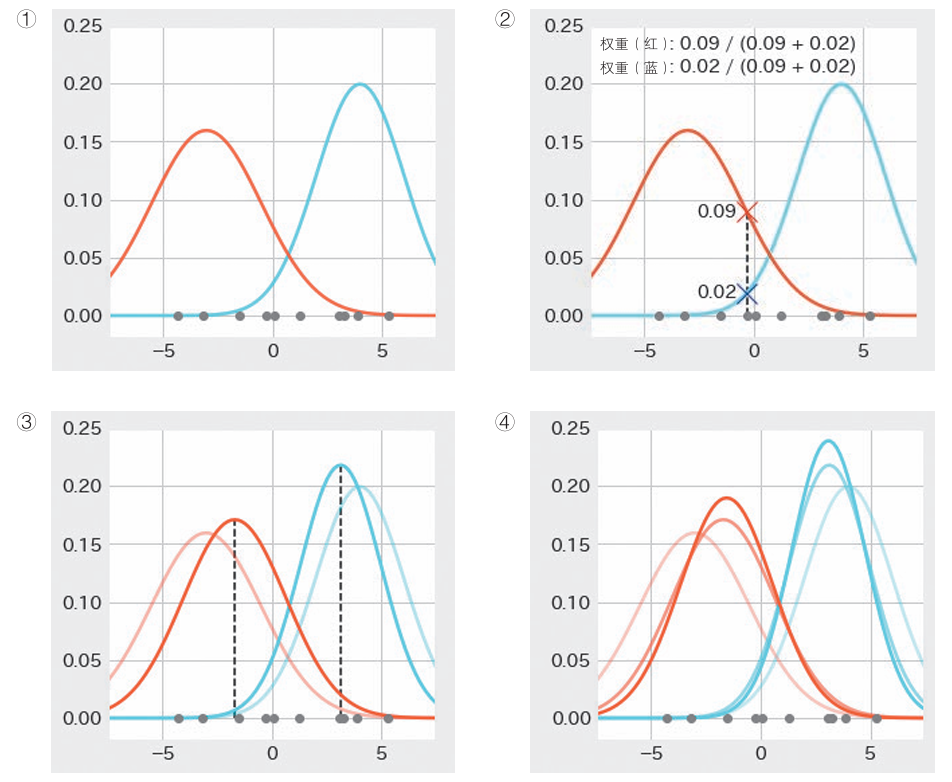
image.png

求解权重和参数通常使用期望最大化（Expectation-Maximization, EM）算法。在不知道数据点的类别标签的情况下，通过反复迭代估计权重和更新参数来逼近真实的高斯分布参数。

在步骤2中计算数据点拥有的权重，权重计算方法为“每个高斯分布的值/所有高斯分布的值之和“。当计算出所有数据点的权重后，求出每个类别的权重的均值，然后计算方差。

示例代码

from sklearn.datasets import load_iris
from sklearn.mixture import GaussianMixture
data = load_iris()
n_components = 3  # 高斯分布的数量
model = GaussianMixture(n_components=n_components)
model.fit(data.data)
print(model.predict(data.data))  # 预测类别
print(model.means_)  # 各高斯分布的均值
print(model.covariances_)  # 各高斯分布的方差

详细说明

以下是对同一数据使用混合高斯分布和K-means进行聚类。

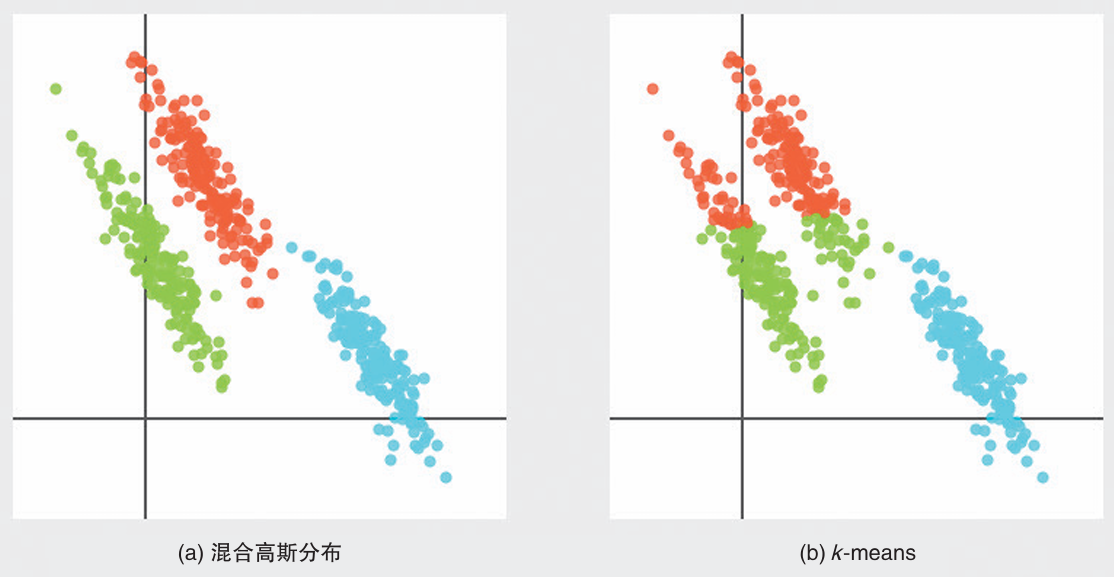
image.png

我们可以看到，混合高斯分布的数据会更优，因为高斯分布对于椭圆形数据更优，而k-means对重心开始呈圆形分布的数据会更好，因此椭圆成为了k-means的软肋，更该使用混合高斯分布。

算法七：LLE

概述

无监督学习中的一项重要任务是将结构复杂的数据转化为更简单的形式。

LLE（Locally Linear Embedding，局部线性嵌入）可以将以弯曲或扭曲的状态埋藏在高维空间中的结构简单地表示在低维空间中。

LLE被称为流形学习，它的目标是对具有非线性结构的数据进行降维。

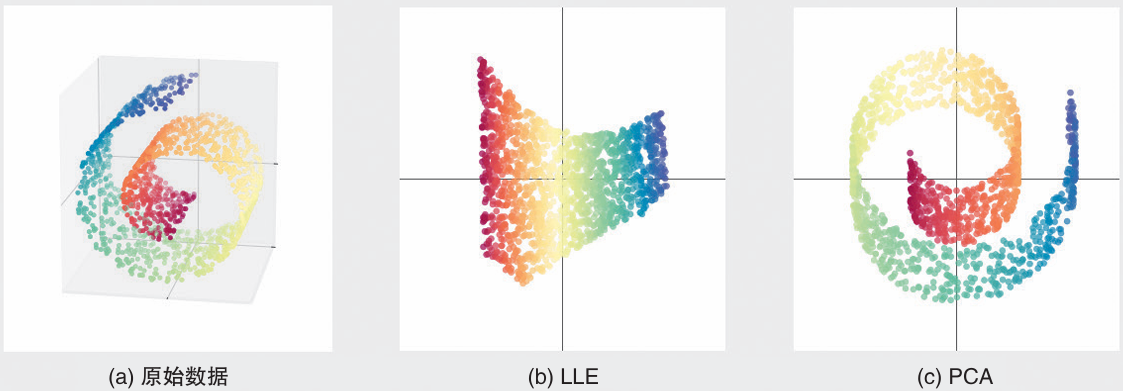
对于原始数据，是典型的瑞士卷数据集图像。LLE和PCA的降维结果如下所示。PCA更像简单的压扁，由于PCA更适合变量之间有一定关联性的数据，所以在降维时，LLE更适合。

image.png

算法说明

LLE 是以降维后依旧保持原始高维空间中的局部线性组合关系作为核心

LLE算法要求数据点由其近邻点的线性组合来表示

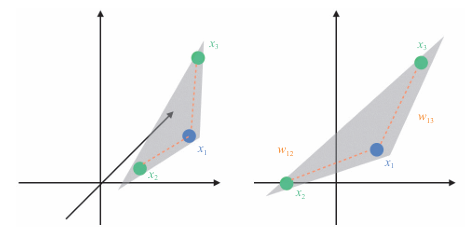
对于数据点 x1，以最接近 x1 的两个点 x2 和 x3 的线性组合来表示它。

可以得到两个权值w12，w13.

目的是通过降维后，依旧保持这个线性组合关系，如下图所示

LLE将高维的曲折关系转化为邻近点的组合关系。

image.png

对于近邻点数量，是超参数，设定为k个。

步骤：

  • 找到数据点 xi 的 k 个近邻点
  • 求出由 k 个近邻点线性组合的权值
  • 使用权值计算出低维度的 y_i

在确定近邻点数量后，首先，为了求出权重 wij，我们将 xi 和 其近邻点的线性组合 的误差表示为

随着 wij 值的变化，这个误差会增大或减少。

通过计算所有 xi 和线性组合的差的平方和，我们将权重 wij 与误差之间的关系表示为以下误差函数：

除了 wij 近邻点之外，表达式中的值都是 0。另外还有一个约束条件：对于某个 i，有

我们可以认为权重 wij 表示数据点 xi 及其近邻点之间的关系，而 LLE 通过这种关系在低维空间中也得以保持。在计算完权重后，我们计算低维空间中表示数据点的 y_i：

前面求出使误差最小的权重 wij，现在要做的是利用刚刚求出的 wij，求使误差最小的 y

示例代码

from sklearn.datasets import samples_generator
from sklearn.manifold import LocallyLinearEmbedding
data, color = samples_generator.make_swiss_roll(n_samples=1500)
n_neighbors = 12  # 近邻点的数量
n_components = 2  # 降维后的维度
model = LocallyLinearEmbedding(n_neighbors=n_neighbors,
n_components=n_components)
model.fit(data)
print(model.transform(data))  # 变换后的数

详细说明

流形学习

流形指的是可以将局部看做没有弯曲的空间，类似于将地球的局部绘制平面地图

“所谓的流形就是从局部来看是低维空间的结构被埋藏在高维空间里”

近邻点数量

近邻点数量是超参数，对于不同的数量有不同的降维结果。如下图

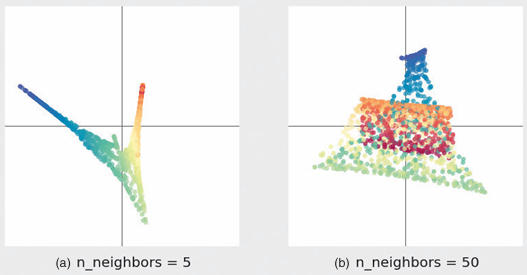
image.png

当近邻点设置为5时，LLT没有连贯的结构，分布狭窄，反应信息少。

当近邻点设置为50时，不同颜色的点距离很近，无法把握局部结构。

这个参数十分重要，影响很大。

算法八：t-SNE

是一种将高维的复杂数据降维为二维（或三维）的算法，用于低维空间的可视化。

概述

t-SNE是一种流形学习算法，用于可视化复杂数据。如下例子是将三维空间上的两个瑞士卷数据转变为二维空间的示例。

image.png

在上图体现出，t-SNE可以在低维空间展现多个结构。

算法说明

步骤：

  1. 对于所有的组 i、j，使用高斯分布来表示 xi 和 xj 的相似度
  2. 在低维空间中随机配置与 x i 相同数量的点 y i，对于所有的组 i、j，使用 t 分布表示 y i 和 y j 的相似度。
  3. 更新数据点 yi，使得步骤 1 和步骤 2 中定义的相似度分布尽可能相似。
  4. 重复步骤 3，直到达到收敛条件。

image.png

相似度指的是 数据点之间的相似程度，使用上图的概率分布衡量。

横轴是距离，纵轴是相似度，越近越相似。

在降低维度的情况下，使他们的相似度保持不变，这就是t-SNE的降维逻辑，此时使用的是 t 分布。

为了在低维空间中更好地表现数据点之间的距离关系，t-SNE并未简单地在高维空间和低维空间中使用相同的概率分布，而是采用了不同的方式：在高维空间中使用高斯分布来计算数据点的相似度，而在低维空间中使用t分布来衡量相似度。

选择t分布的原因在于它的重尾特性，这使得在低维空间中远离某个聚类中心的点不容易被压缩到中心附近，从而保持了聚类之间的分离度。因此，在低维空间中，数据点的相似度分布可以更自然地反映出聚类结构，使得不同聚类之间的距离更加明显。

在这个过程中，t-SNE通过最小化KL散度（Kullback-Leibler散度）来度量高维和低维空间相似度分布之间的差异，从而在降维过程中尽量保持高维空间中的相似度关系。这种方法使得t-SNE能够在低维空间中还原数据的高维结构，同时使聚类和局部关系更为清晰。

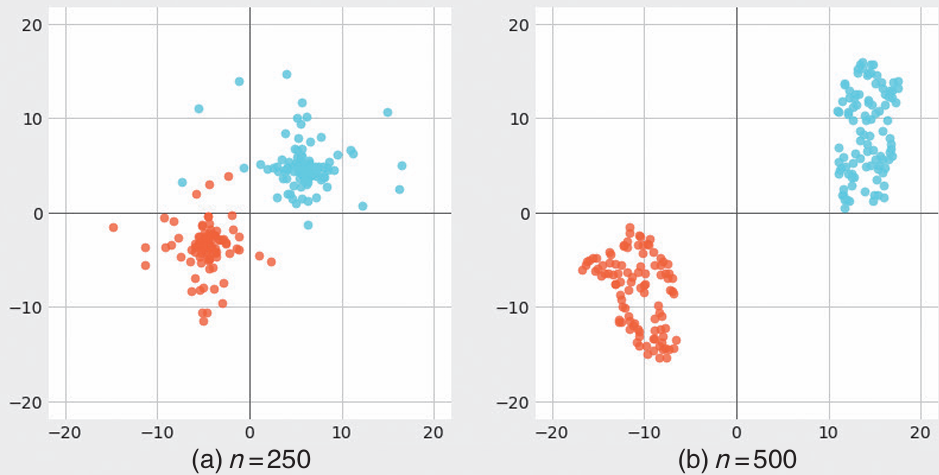
image.png

如上为更新次数是250和500的情况。

t-SNE通常用于降维到三维或者二维，在高维空间中，远离重心的点占主导地位，局部信息无法保留，因此无法降维到四维或者更高空间。

示例代码

from sklearn.manifold import TSNE
from sklearn.datasets import load_digits
data = load_digits()
n_components = 2  # 设置降维后的维度为2
model = TSNE(n_components=n_components)
print(model.fit_transform(data.data))

详细说明

使用手写数组数据作为训练数据，对PCA，LLE，t-SNE三种方法进行降维，展现结果如下：

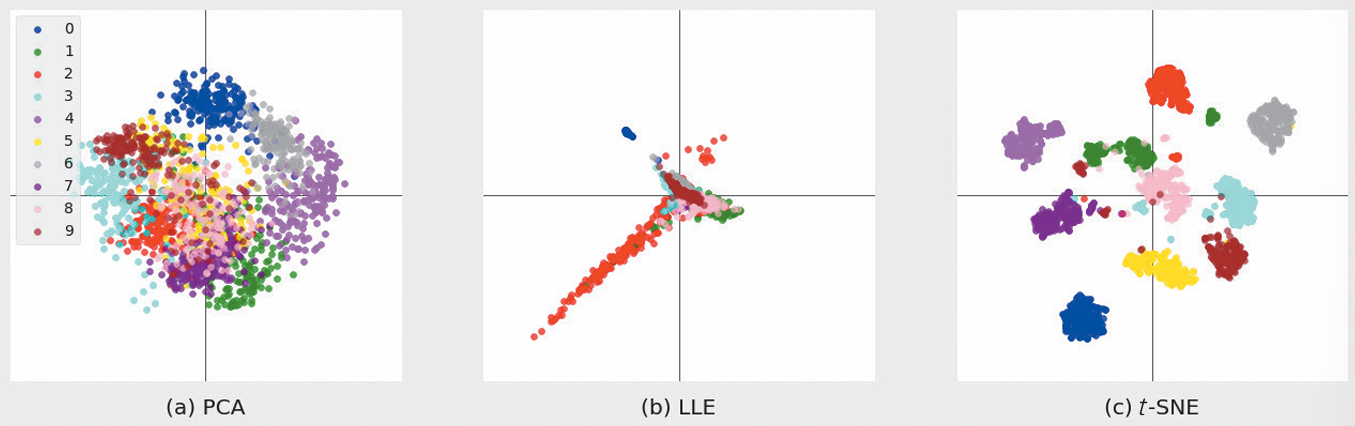
image.png

PCA虽然进行归类，但很混杂。

LLE适用于非线性数据，但如果数据不是像瑞士卷一样几种，就不能很好把握结构。

t-SNE 在二维空间进行了很好的分类。