这篇文章上次修改于 211 天前,可能其部分内容已经发生变化,如有疑问可询问作者。
算法一:PCA
概述
是一种降维算法,可以将相关的多变量数据以主成分简洁地表现出来。
它对变量之间存在相关性的数据很有效。
对减少数据的方法:
- 只选择重要变量,舍弃其余变量
- 基于原变量构造新变量(PCA使用)
概念:
- 降维:指在保留数据特征的前提下,以少量的变量表示有许多变量的数据,这有助于降低多变量数据分析的复杂度。
- 主成分:低维变量表示高维空间中的数据后,低维的轴叫作主成分
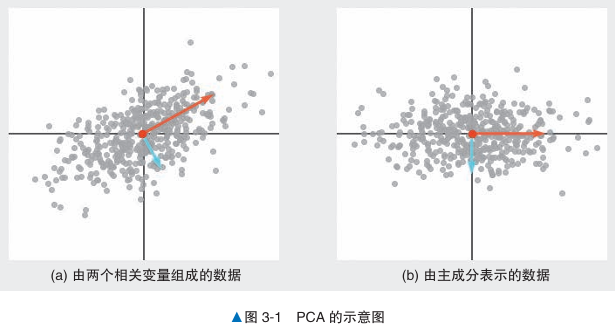
- 方向:对散点图使用PCA得到两个正交的向量,线的方向表示数据的方向
- 重要度:两个正交的向量,线的长度表示重要度(如下图)
- 主成分得分:图3-1b 是以这两条线为新轴对原始数据进行变换后得到的图形,变换后的数据称为主成分得分
- 第一(二)主成分:主成分轴的重要度的值从高到低排序。第一主成分包含了更多原始数据的特点。
算法说明:
特征值问题
是在线性代数中分析矩阵性质的重要问题,涉及找到矩阵的特征值和对应的特征向量
给定一个 的方阵 ,特征值问题的目标是找到一个标量 λ 和一个非零向量 v,使得:
其中:
- λ 是矩阵 A 的特征值。
- v 是矩阵 A 的对应特征向量。
这表示矩阵 A 对特征向量 v 的作用只是将其放缩,而不改变其方向。特征值问题可以转换为以下形式:
其中 I 是单位矩阵。要使这个方程有非零解 v,需要矩阵 是奇异的,即它的行列式为零。因此,特征值 λ 满足以下特征方程:
解这个方程可以得到所有的特征值 λ,然后将这些值代入 可以得到对应的特征向量 v。
特征向量是指经过矩阵变换后不改变方向的向量,而特征值表示在这种变换下该向量的缩放比例。
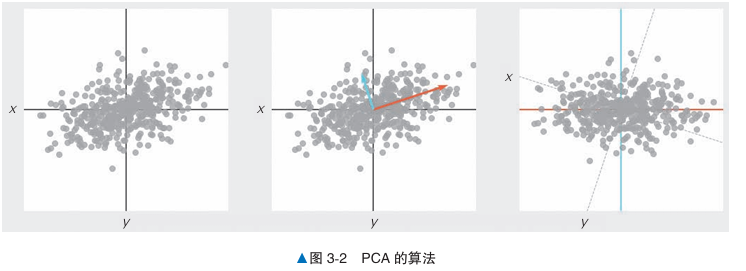
步骤:
- 计算协方差矩阵
- 对协方差矩阵求解特征值问题,求解特征向量和特征值
- 以数据表示各主成分方向
什么是协方差矩阵
协方差矩阵表示了多维数据集中每对变量之间的协方差。协方差衡量两个变量的关系——如果两个变量的协方差为正,说明它们通常同向变化(一个增加时另一个也增加);如果为负,说明它们反向变化;协方差为零表示两个变量之间没有线性关系。
假设有 n 个变量 ,它们组成一个随机向量
。协方差矩阵 Σ 的每个元素
是变量
和
的协方差:
协方差矩阵的大小是 ,其中 n 是变量的数量。
如何计算协方差矩阵
设我们有一个数据集,包含 m 个样本,每个样本有 n 个特征,可以用矩阵 X 表示该数据集,其中 X 的维度为 (行表示样本,列表示特征)。
- 计算每个变量的均值:首先对每个变量(列)计算均值向量
,其大小为
。
- 去中心化数据:将每个样本减去对应变量的均值。生成一个新的矩阵 X’,其中
。
- 计算协方差矩阵:协方差矩阵 Σ 通过以下公式计算:
这里
是去中心化数据的转置,乘积
计算了每对变量之间的协方差。
这样得到的协方差矩阵 Σ 是一个 对称矩阵。
在主成分分析(PCA)中,协方差矩阵 A 的特征值和特征向量用于提取数据的主要方向和重要性。
- 协方差矩阵:在 PCA 中,数据的协方差矩阵 AAA 描述了各个特征之间的相关性。这一矩阵的特征值和特征向量揭示了数据在各个方向上的变动程度。
- 特征值和特征向量:对协方差矩阵求解特征值问题,得到了一组特征值和对应的特征向量。排序后,每个特征向量按特征值大小表示一个主成分,即数据的主要变化方向。第一个特征向量对应于数据的最大变化方向(第一主成分),第二个特征向量对应次大的变化方向(第二主成分),以此类推。
- 贡献率:特征值的大小反映了每个主成分对数据的解释能力。通过计算每个特征值与特征值总和的比值(即贡献率),可以用百分比表示每个主成分的重要性,反映其对数据变异的解释能力。
- 累计贡献率:按主成分的重要性顺序将贡献率累加,可以得到累计贡献率。一般在 PCA 中选择累计贡献率达到某个阈值(如 90% 或 95%)的主成分数量,以确保在降低维度的同时尽可能多地保留数据的信息。
示例代码
from sklearn.decomposition import PCA
from sklearn.datasets import load_iris
data = load_iris()
n_components = 2 # 将减少后的维度设置为2
model = PCA(n_components=n_components)
model = model.fit(data.data)
print(model.transform(data.data)) # 变换后的数据详细说明
主成分的选择方法
对于主成分,先设定一个基准值,当前几累积主成分的贡献值达到基准值,就可以决定要选择主成分的数量。
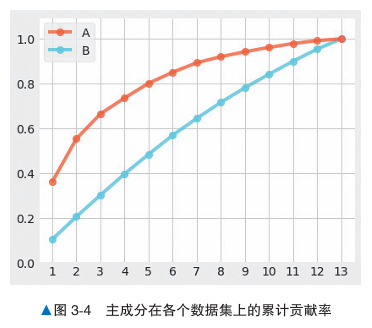
对于下图,纵轴是累计主成分,横轴是主成分数据数量。
A数据的数据相关性较强,出现曲线机制。
B数据的数据相关性较弱,多个主成分的贡献值一致,不适合使用PCA进行降维。
算法二:LSA
概述
LSA(Latent Semantic Analysis,潜在语义分析)是一种自然语言处理技术,常用于信息搜索领域。
作为一种降维算法,它能够从大量文本数据中找出单词之间的潜在关联性。
基于关键词匹配的传统信息检索方法
- 将文本数据中的所有单词提取出来,建立一个索引结构。索引类似于目录,每个单词对应一个列表,记录了该单词在不同文本(例如在文本1 3出现)中的出现位置。
- 用户输入搜索关键词后,系统在索引中查找与该关键词完全相同的单词。返回对应的列表作为搜索结果。
不足:
无法判断同义词。例如,“深度学习”和“机器学习”在语义上相关,但它们的关键词不同,无法匹配到相同的结果。
LSA信息检索和语义空间
LSA可以根据文本计算单词之间的相似度,以及单词和文本的相似度。
通过LSA对文本和单词的矩阵进行降维,将其变换为潜在语义空间。这种变换使用矩阵分解进行。(矩阵分解是指将某个矩阵表示为多个矩阵的乘积的形式。)
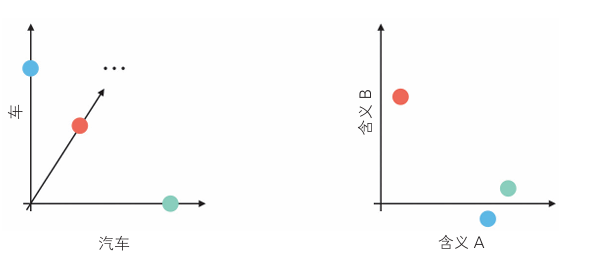
- 左图:单词空间,车和汽车相关度为0,两者正交不相干
- 右图:语义空间,两者向量非常接近,内积值接近1,表明它们语义高度相关。
!
算法说明
以下结合具体例子
首先将以下文本变换为矩阵。矩阵
的各元素是文本中出现的单词的个数。
- 文本1:坐汽车去公司
- 文本2:坐车去的
- 文本3:在餐厅吃汉堡牛肉饼
- 文本4:在餐厅吃意大利面
| 文本1 | 文本2 | 文本3 | 文本4 | |
|---|---|---|---|---|
| 汽车 | 1 | 0 | 0 | 0 |
| 公司 | 1 | 0 | 0 | 0 |
| 去 | 1 | 1 | 0 | 0 |
| 车 | 0 | 1 | 0 | 0 |
| 餐厅 | 0 | 0 | 1 | 1 |
| 汉堡牛肉饼 | 0 | 0 | 1 | 0 |
| 吃 | 0 | 0 | 1 | 1 |
| 意大利面 | 0 | 0 | 0 | 1 |
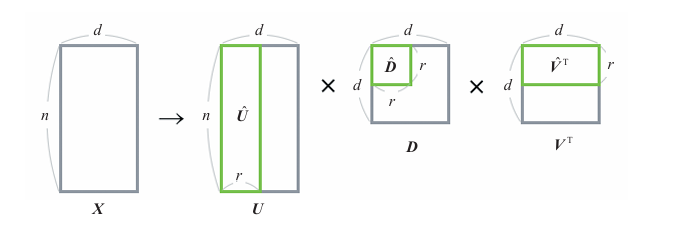
上图为矩阵X,对矩阵X分解后得:
矩阵解释:
是包含单词和归纳的特征的变换信息的矩阵
是包含信息的重要度的矩阵,是一个对角矩阵,其对角元素按信息的重要度从大到小排列。
是包含归纳的特征和文本的变换信息的矩阵
降维
原始数据有4个特征,但我们希望将其降维到2个特征。
从的4个值中选出最重要的2个:建立一个2行2列的对角矩阵。
为了匹配这个,我们相应地删去
的第3列和第4列,以及
的第3列和第4列,将它们分别变形为8行2列和2行4列的矩阵。
该矩阵乘积是原矩阵的近似,即使只用了一半的值,还是在一定程度上保留了原来的信息。
当作为降维算法使用时,我们要用到的是在变换为原始特征的形式之前(在乘以之前)的
。
是一个8行2列的矩阵,我们可以将其解释为从归纳的特征中选择的2个重要度高的特征。
以下是关于的具体数值,将两个特征设为A和B。
| A | B | |
|---|---|---|
| 汽车 | 0.00 | 0.85 |
| 公司 | 0.00 | 0.85 |
| 去 | 0.00 | 1.38 |
| 车 | 0.00 | 0.53 |
| 餐厅 | 1.41 | 0.00 |
| 汉堡牛肉饼 | 0.71 | 0.00 |
| 吃 | 1.41 | 0.00 |
| 意大利面 | 0.71 | 0.00 |
“汽车”和“车”拥有变量B的值,“汉堡牛肉饼”和“意大利面”拥有变量A的值。A和B的特征值显示了各个单词之间的关联性。
示例代码
假设一个使用8个变量(=单词的个数)表示的数据集,现用2个潜在变量去表示它。
from sklearn.decomposition import TruncatedSVD
data = [[1, 0, 0, 0],
[1, 0, 0, 0],
[1, 1, 0, 0],
[0, 1, 0, 0],
[0, 0, 1, 1],
[0, 0, 1, 0],
[0, 0, 1, 1],
[0, 0, 0, 1]]
n_components = 2 # 潜在变量的个数
model = TruncatedSVD(n_components=n_components)
model.fit(data)
print(model.transform(data)) # 变换后的数据
print(model.explained_variance_ratio_) # 贡献率
print(sum(model.explained_variance_ratio_)) # 累计贡献率另外,与PCA一样,我们也可以检查LSA变换后的矩阵中包含多少原始信息。使用了scikit-learn的上述代码输出的累计贡献率约为0.67,表明这2个变量包含了约67%的原始数据的信息。
详细说明
使用LSA时的注意事项
本矩阵分解是奇异值分解。
它具有以新的空间表示文本等优点。但有以下问题:
- 变换后的矩阵难以解释。在通过奇异值分解降维时,各个维度可能是正交的,矩阵中的元素也可能是负值。
- LSA的计算成本有时很高。单词个数与维度相关,可能会有非常大的矩阵。
- 更新难度大,随着新词加入,原有矩阵需重建。
算法三:NMF
概述
NMF(Non-negative Martix Factorization,非负矩阵分解)是一种降维算法也是一种矩阵分解方法。
NMF有以下特点:
- 原始矩阵的元素和分解后矩阵的元素是非负数
- 没有“潜在语义空间的每一个维度都是正交的”这一约束条件
以下分别为对二维数据应用NMF和PCA的结果。
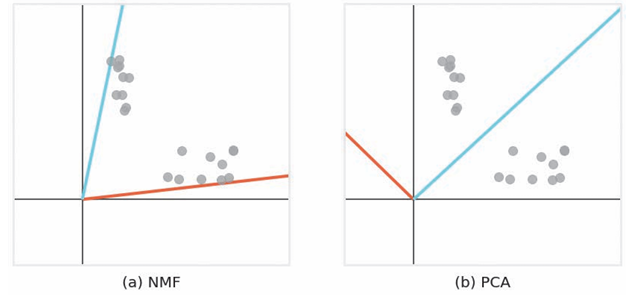
可以看出NMF的潜在空间的每个轴会靠近密集的点,使得轴上有重复信息。这一特性使得我们可以捕捉到多个数据块的特征。
而PCA等算法则由于其潜在空间的维度是正交的,所以无法找到所有数据块的特征。
算法说明
实例
假设我们有以下三篇文档:
- 文档1:谈论人工智能和机器学习。
- 文档2:讨论深度学习和神经网络。
- 文档3:介绍数据分析和统计学。
通过 NMF,可以将文档表示为某些“主题”的线性组合。例如:
- 主题A:与“人工智能、机器学习”相关。
- 主题B:与“统计学、数据分析”相关。
- 主题C:与“深度学习、神经网络”相关。
NMF 的结果可能如下:
- 文档1 ≈ 0.6 × 主题A + 0.3 × 主题C
- 文档2 ≈ 0.8 × 主题C + 0.1 × 主题A
- 文档3 ≈ 0.7 × 主题B + 0.2 × 主题A
这个表示让我们可以用主题分布来描述每篇文档,比如:
- 文档1的“主题A贡献”为0.6,“主题C贡献”为0.3。
抽象化
设原始数据为行
列的矩阵
。将其表示为两个矩阵
和
的乘积。
是
行
列的矩阵,是一个 文档 - 主题 矩阵每一行表示一个文档在不同主题上的权重。
是
行
列的矩阵,每一列表示一个主题在各个词汇上的权重。
是原始矩阵
的近似,选择比
小的
就可以进行降维。
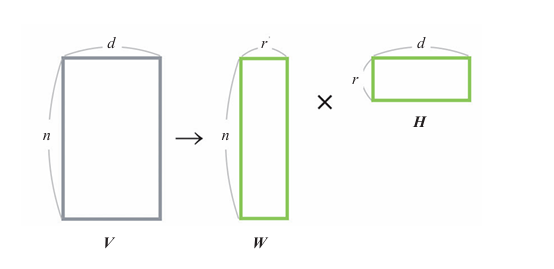
在求和
的过程中,NMF在
的条件下,使
接近
。
NMF采取“将视为常数,更新
”“ 将
视为常数,更新
”的方式交替更新
和
.
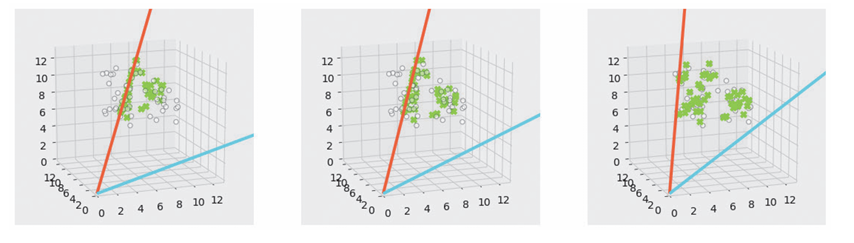
以下对NMF过程进行可视化。
灰色的点为原始矩阵,绿色的点为近似矩阵
。随着计算的进行,我们可以看到近似矩阵越来越接近原始矩阵。此外,红线和蓝线是潜在空间的轴,所有近似矩阵的图形都能在潜在空间(二维空间)的轴上表示出来
-
将
和
初始化为正值。
-
将
视为常数,更新
。
-
将
视为常数,更新
。
-
当
和
收敛时,停止计算。
示例代码
from sklearn.decomposition import NMF
from sklearn.datasets.samples_generator import make_blobs
centers = [[5, 10, 5], [10, 4, 10], [6, 8, 8]]
V, _ = make_blobs(centers=centers) # 以centers为中心生成数据
n_components = 2 # 潜在变量的个数
model = NMF(n_components=n_components)
model.fit(V)
W = model.transform(V) # 分解后的矩阵
H = model.components_
print(W)
print(H)详细说明
NMF与PCA的比较
将NMF和PCA应用到一个人脸数据集上(19像素×19像素,2429张),降维后由49个变量表示数据。即将361个特征变换为49个潜在变量。
将49个潜在变量可视化
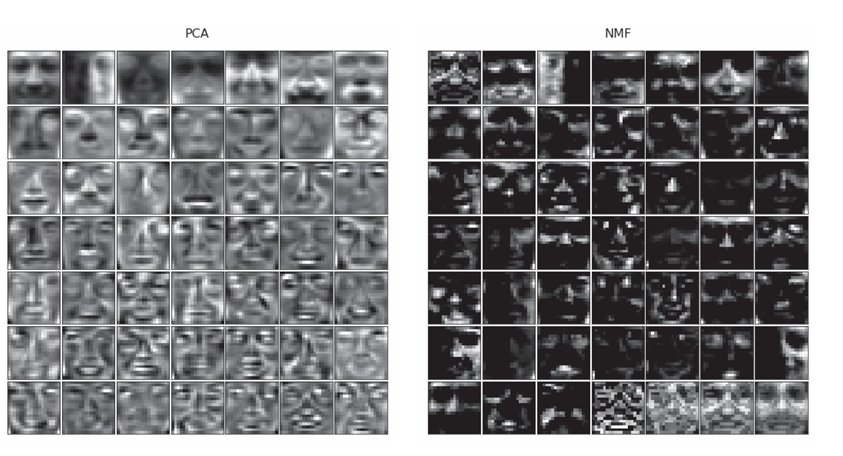
左图为PCA结果,每张图像表示了人的整个面部,负值暗,正值亮。PCA通过将不同的脸加在一起恢复原始图像。
右图为NMF的结果,暗区较多,但这些区域的值为0.。每个潜在变量代表了人脸的一部分特征。NMF通过组合具有人脸部分特征的图像来回复原始图像,NMF的潜在变量含义可解释性更强,能够清晰地反映数据的实际意义和结构。
算法四:LDA
概述
LDA(Latent Dirichlet Allocation)是一种降维的用于文本建模的算法。可根据文本中的单词找出潜在的主题并分类。
举个例子
- We go to school on weekdays.
- I like playing sports.
- They enjoyed playing sports in school.
- Did she go there after school?
- He read the sports columns yesterday
假设这些例句主题数为2,将其应用于LDA算法。
以下为主题A和主题B单词的概率分布
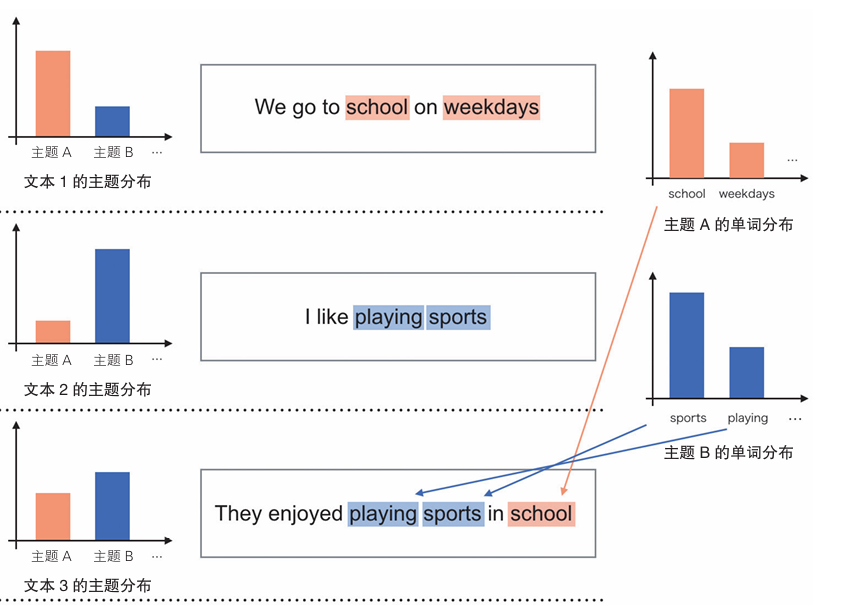
school是主题A的代表性单词,sports是主题B的代表性单词
具体做法如下:
- 基于文本的主题分布为单词分配主题
- 基于分配的主题的单词分布确定单词
- 对所有文本中包含的单词执行步骤1和步骤2的操作
算法说明
LDA通过以下步骤计算主题分布和单词分布。
- 为各文本的单词随机分配主题。
- 基于为单词分配的主题,计算每个文本的主题概率。
- 基于为单词分配的主题,计算每个主题的单词概率。
- 计算步骤2和步骤 3中的概率的乘积,基于得到的概率,再次为各文本的单词分配主题。
- 重复步骤2 ~ 步骤4的计算,直到收敛。
示例代码
from sklearn.datasets import fetch_20newsgroups
from sklearn.feature_extraction.text import CountVectorizer
from sklearn.decomposition import LatentDirichletAllocation
# 使用remove去除正文以外的信息
data = fetch_20newsgroups(remove=('headers', 'footers', 'quotes'))
max_features = 1000
# 将文本数据变换为向量
tf_vectorizer = CountVectorizer(max_features=max_features,
stop_words='english')
tf = tf_vectorizer.fit_transform(data.data)
n_topics = 20
model = LatentDirichletAllocation(n_components=n_topics)
model.fit(tf)
print(model.components_) # 各主题包含的单词的分布
print(model.transform(tf)) # 使用主题描述的文本使用scikit-learn实现基于LDA的主题模型的创建。使用了一个名为20 Newsgroups的 数据集,这个数据集是20个主题的新闻组文本的集合,每个文本属于一个主题。
详细说明
使用主题描述文本
一些主题能直观地通过包含的单词来概述文本,比如 game team year games season play hockey players league win teams 是关于体育的。
一些只包含数值或概括性不强的单词的主题则通过停用词(为了提高精度而排除在外的单词)来进行改进。
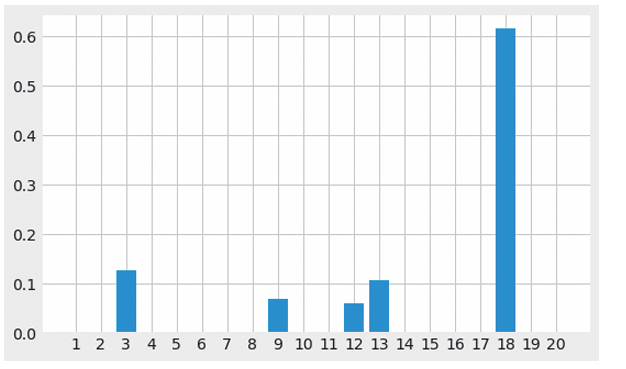
以上是文本的主题分布图,可以明显直观地看出是主题18的文本。