这篇文章上次修改于 275 天前，可能其部分内容已经发生变化，如有疑问可询问作者。

算法学习笔记(14):AC自动机

这名字听起来也太高级了，但实际上就是KMP+TIRE树。

所以不妨别管这个名字（Aho–Corasick Automaton）

实际上目的是多字符串匹配查找。

对于字符串，先要了解一些术语，为了方便之后描述。

模式匹配：也就是字符串匹配问题，在主串中寻找子串。
模式串：用于查找的字符串，例如114514中找45，45就是模式串
待匹配串：114514
多串匹配：多个模式串和一个待匹配串的匹配问题

AC自动机解决的是多串匹配问题。

思想构建

首先由于是多串问题，对于多串匹配，也就是多模式匹配，我们需要存储多个模式，例如n个串，在匹配的过程中我们要存储n个匹配状态，以及保存n个模式串的内容。

其次再考虑匹配问题，AC自动机还是离不开KMP算法的思想，回顾KMP算法的思路，KMP主要注重减少重复的匹配，何为重复的匹配，也就是我们匹配的过程中，能否省略掉已经匹配的部分，减少匹配次数。

多串问题解决

对于多个串，我们可以利用字典树，字典树利用的是字符串的字符种类个数有限的特性，对于多个模式串统一到了字典树之中，此时再讨论匹配状态，可以发现所有的匹配状态都统一了。对于一个起点，一个一个字符的匹配就相当于走树，走到某个节点就是匹配到了哪一个部分，走过了哪个模式串就是这个模式串匹配成功。字典树很好的处理了多串问题，将多串化繁为简。

而且如果两个模式串都有公共前缀abc，那么在匹配的时候就会被同时考虑。

匹配问题解决

使用了字典树把问题转移到了枚举每个起点，来寻找匹配。这是肉眼可见的暴力的，这是可以优化的。优化思路同KMP，减少匹配次数，利用字符串的重复性。

先回顾KMP算法再来这里开始看。

回顾KMP：在ABABABCAA 中寻找 ABABC，在被匹配串匹配到第五个字符A和模式串C不匹配，下一步从第三个字符开始比对。因为第34个字符是AB，依靠next数组直接跳到了第三个字符进行比较。

对于字典树能否也找到减少匹配的优化点呢？（甚至比KMP更好理解）

假设我已经匹配了前面的部分 ABCDE，下一个字符F无法匹配了。此时，我们寻找是否有模式串以BCDE开头；如果有，从BCDE开始匹配，如果没有，看看CDE，没有再看看DE，E，都没有，决定从头开始。

不同于KMP，多串匹配有更多的可能性可以重复利用已经比较过的部分，KMP只能通过ABAB，自身的相同来省略。例如多模式匹配，可能有ABCDE，BCDE，CDE，可以重复利用的机会更大。

步骤上来说，实际上是不断放弃前缀，看看能否利用，能利用，则跳转过去。

这种跳转的行为模式和 KMP的next数组跳转是一样的，目的就是利用已经匹配的部分。

在KMP中被称作next，在AC自动机中我们称作失陪指针，又叫fail指针，当这次匹配失败，就该到哪里开始。

根据以上思想，我们可以有以下图（from BV14v4y1Z7fu）：

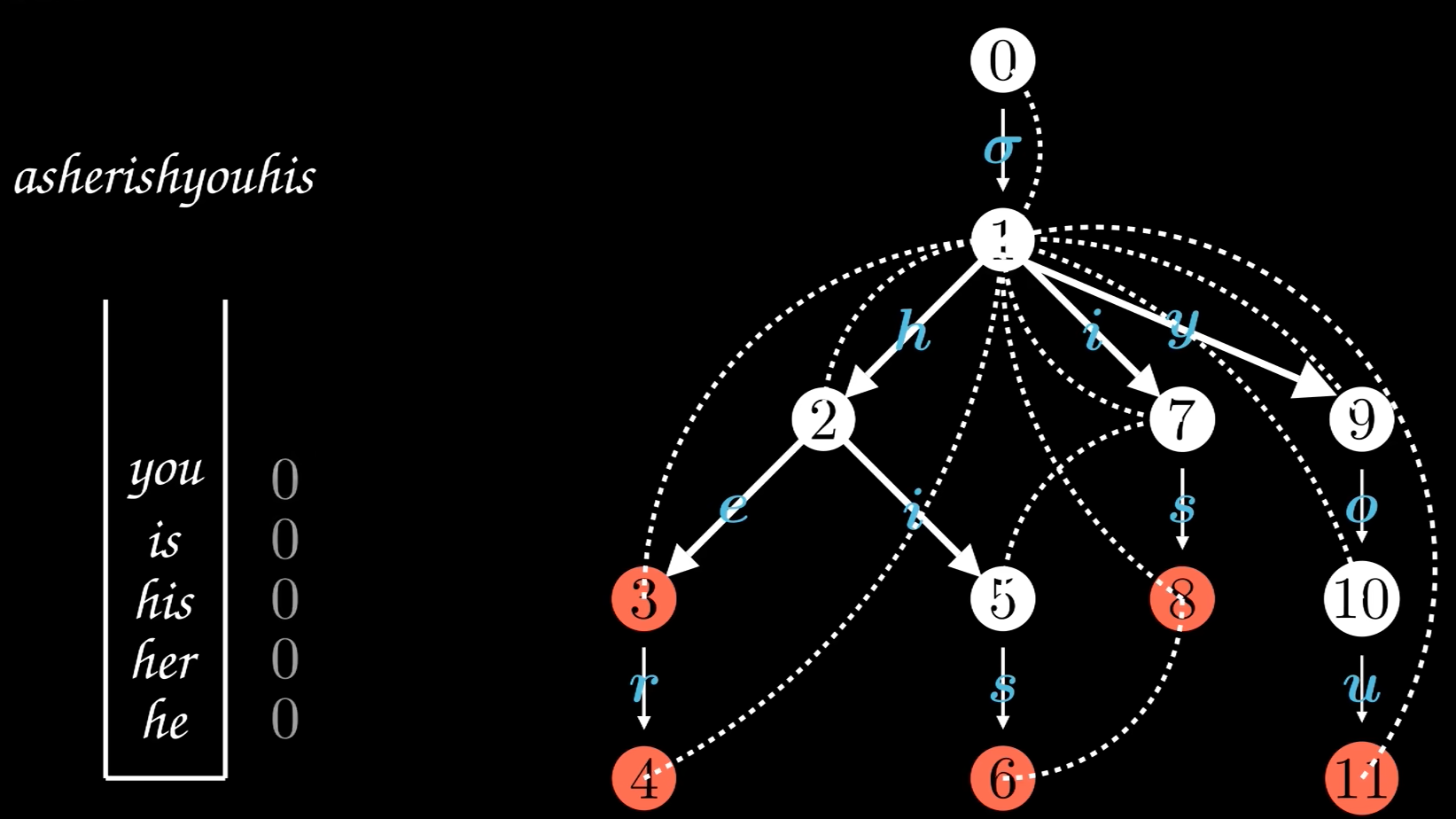
左边的词就是我们的多个模式子串，而右边就是我们构造的字典树，其中虚线就是我们的失配指针（fail指针），虚线看起来事很复杂繁乱的，但我们只需要注意其中的几个。

例如节点5，当我们匹配到节点5失败后，应当跳转到节点7：

因为到5的时候已经有hi成功，这时候放弃前缀h，看看有没有i开始的，也就是从节点7开始。

例如节点6，当我们匹配到节点6的时候，应当跳转到节点8：

因为到6的时候已经满足了his，放弃前缀h，看看有没有is开始的，也就是8.

例如节点11，应当跳转到节点1：

到11的时候满足了you，放弃前缀，看看ou有没有，没有则看看u有没有，没有就从头开始。

实际上很好理解，接下来考虑fail指针如何构建。

失配指针构建(fail指针)

由上可知，失配指针永远都是从深度更深到更低的，也就是说，我们在处理深度更深的指针时，已经处理了深度更小的指针。因此我们采用BFS的思路来构建。

再考虑子节点的指针和父节点指针的关系：

例如上图中的5,6，我们可以发现，6的指针就是在5的指针下，走了s的一步。

但如果没有s的这一步呢（没有7 - 8 是 s 的边）？如果7-8 是 p，那么6的指针就是起点。

根据我们的放弃前缀解释，我们要找放弃最短前缀（转移后最长）的一次转移。（强调）

见代码中体现：

// 失配指针数组
int failPtr[MAXS]; 
  
// g[a][ch] 的意思是从状态点a 通过字符ch的边到达的状态值
int g[MAXS][MAXC]; 
 
int buildMatchingMachine(string arr[], int k) 
{ 
    // 初始化
    memset(out, 0, sizeof out); 
    memset(g, -1, sizeof g); 
  
    // 一开始我们只有0个状态值
    int states = 1; 

    // 构造字典树
    for (int i = 0; i < k; ++i) 
    { 
        const string &word = arr[i]; 
        int currentState = 0; 
        for (int j = 0; j < word.size(); ++j) 
        { 
            int ch = word[j] - 'a'; 
            if (g[currentState][ch] == -1) 
                g[currentState][ch] = states++; 
            currentState = g[currentState][ch]; 
        }
        // 可以为最后一个字符位置加标记。
		 }
  
    // 对于所有在Trie中没有根边(或状态0)的字符，在状态0本身添加一条goto边
    for (int ch = 0; ch < MAXC; ++ch) 
        if (g[0][ch] == -1) 
            g[0][ch] = 0; 
  
    // 开始构建失配指针
  
    memset(failPtr, -1, sizeof failPtr); 
  
    // 失配指针构建使用BFS构建
    queue<int> q; 
  
    // 迭代所有可能的字符
    for (int ch = 0; ch < MAXC; ++ch) 
    { 
        // 深度为1的失配指针都是指向0的起点
        if (g[0][ch] != 0) 
        { 
            failPtr[g[0][ch]] = 0; 
            q.push(g[0][ch]); 
        } 
    } 
  
    while (q.size()) 
    { 
        int state = q.front(); 
        q.pop(); 
  
        // 对于已删除状态，为所有未定义goto函数的字符查找失败函数。
        for (int ch = 0; ch <= MAXC; ++ch) 
        { 
            if (g[state][ch] != -1) 
            { 
                int failure = failPtr[state]; 
                
                // 找到从根到当前状态的字符串的适当后缀标记的最深节点
                while (g[failure][ch] == -1) 
                      failure = failPtr[failure]; 
  
                failure = g[failure][ch]; 
                failPtr[g[state][ch]] = failure; 

                q.push(g[state][ch]); 
            } 
        } 
    } 
    return states; 
}

tps：仅供参考学习，不建议作为板子

查询就十分简单了：

int findNextState(int currentState, char nextInput) 
{ 
    int answer = currentState; 
    int ch = nextInput - 'a'; 
    
    while (g[answer][ch] == -1) 
        answer = failPtr[answer]; 
        
    return g[answer][ch]; 
} 
  

void searchWords(string arr[], int k, string text) 
{ 
    buildMatchingMachine(arr, k); 
    int currentState = 0; 
    for (int i = 0; i < text.size(); ++i) 
    { 
        currentState = findNextState(currentState, text[i]); 
			  // 如果当前状态值是被标记的状态值，就代表匹配了一次字符串
    } 
}

参考代码2：(计算所有子串的出现次数之和)

#include <bits/stdc++.h>
using namespace std;
const int N = 1e6 + 6;
int n;

int tr[N][26], tot;
int strEnd[N], fail[N];

void insert(const string & str)
{
    int cur = 0;
    for (char ch : str)
    {
        if (!tr[cur][ch - 'a']){
            tr[cur][ch - 'a'] = ++tot;
        }
        cur = tr[cur][ch - 'a'];
    }
    strEnd[cur]++;
}

void build()
{
    queue<int> BFSque;
    for (int i = 0; i < 26; i++)
        if (tr[0][i])
            BFSque.push(tr[0][i]);
    
    while (BFSque.size())
    {
        int cur = BFSque.front(); BFSque.pop();
        
        for (int i = 0; i < 26; i++)
        {
            if (tr[cur][i])
            {
                fail[tr[cur][i]] = tr[fail[cur]][i];
                BFSque.push(tr[cur][i]);
            }
            else{
                tr[cur][i] = tr[fail[cur]][i];
            }
        }
    }
}

int query(const string & text)
{
    int u = 0, res = 0;
    for (char c:text)
    {
        u = tr[u][c - 'a'];
        for (int j = u; j && strEnd[j] != -1; j = fail[j])
        {
            res += strEnd[j], strEnd[j] = -1;
        }
    }
    return res;
}

对于这个问题，当我们匹配成功了ABCD的时候实际上BCD也成功匹配了，需要把所有后缀都进行计数。为什么不在fail了之后再加呢？因为走进下一步的时候已经是ABCDE了，无法计数CD，故在走到ABCD的时候就需要对所有后缀进行统计，而此时的后缀恰恰好就是我们fail指针指向的地方。

优化AC自动机

这两份参考代码如果认真看，可以发现第二份中并没有第一份的while循环，第二份代码把这个while的步骤交给了移动的时候处理。

而对于字符串的计数问题：

这个while的步骤，也就是fail数组往上不断跳跃的部分，这个部分导致了运算的时候反复经过fail跳跃。跳跃不要紧，重要的是要计算的贡献的时候要不断跳跃，计算ABCD的时候要计数BCD，CD, D，计数BBCD的时候也要计数BCD，CD，D。他们走了相同的步骤，所以是一个很大的重复计算。

为了避免不断地向上重复记录，采用懒惰标记，在走到一个fail的时候添加懒惰标记，再在最后把所有fail情况进行一个跳跃讨论。

同时建图的时候考虑fail指针形成的是一个树，并且拓扑排序恰好对应了这个统计过程。

#include <bits/stdc++.h>
#define maxn 2000001
using namespace std;

namespace ACAUTO
{
char s[maxn], T[maxn];
int n, status, vis[200051], ans, in[maxn], Map[maxn];

struct Node
{
    int son[26], fail, flag, ans;
    void clear() { memset(son, 0, sizeof(son)), fail = flag = ans = 0; }
};

Node trie[maxn];
const int ROOT = 1;
const int NONE = 0;

queue<int> q;
void insert(const string & str, int strId)
{   
    int cur = ROOT;
    for (char ch: str)
    {
        int v = ch - 'a';
        if (trie[cur].son[v] == NONE)
            trie[cur].son[v] = ++status; // 为自动机添加状态
        
        cur = trie[cur].son[v];
    }
    if (not trie[cur].flag)
        trie[cur].flag = strId;

    Map[strId] = trie[cur].flag;
}

void getFail()
{
    for (int i = 0; i < 26; i++)
        trie[0].son[i] = ROOT;

    q.push(ROOT);
    while (not q.empty())
    {
        int cur = q.front();
        q.pop();

        int Fail = trie[cur].fail;
        for (int i = 0; i < 26; i++)
        {
            int son = trie[cur].son[i];
            if (trie[cur].son[i] == NONE){
                // 如果没有说明已经匹配失败了，往上跳
                trie[cur].son[i] = trie[Fail].son[i];
            }else{
                // 如果有，就是爹的fail的 相同son位置
                trie[son].fail = trie[Fail].son[i];
                q.push(son);

                in[trie[son].fail]++; // 记录 son 的入度
            }
        }
    }
}

void topu()
{
    for (int i = 1; i <= status; i++)
        if (in[i] == 0)
            q.push(i);
    
    while (!q.empty())
    {
        int cur = q.front();
        q.pop();
        vis[trie[cur].flag] = trie[cur].ans;
        int v = trie[cur].fail;
        in[v]--;
        trie[v].ans += trie[cur].ans;
        if (in[v] == 0)
            q.push(v);
    }
}

void query(const string & str)
{
    int cur = ROOT;
    for (char ch : str){
        cur = trie[cur].son[ch - 'a'];
        trie[cur].ans++;
    }
}

} // namespace ACAUTO

int main()
{   
    using namespace ACAUTO;
    scanf("%d", &n);
    status = 1;
    for (int i = 1; i <= n; i++)
    {
        scanf("%s", s);
        insert(s, i);
    }
    getFail();
    scanf("%s", T);
    query(T);
    topu();
    for (int i = 1; i <= n; i++)
        printf("%d\\n", vis[Map[i]]);
}

学会使用AC自动机后，要能对代码进行各种方面的修改，才算是真正理解。

何为自动机，可以看做是一个机器，机器在工作的时候有诸多状态，比如查询字符串abcd，查询到b位置是一个状态，查询到c位置是一个状态，所以对于我们的AC自动机，字典树上的每个节点就是一个状态。自动机就是在状态之间不断变化而称作自动机。

Mai Icy