算法学习笔记9——后缀数组 2024.04.11 算法学习笔记

这篇文章上次修改于 243 天前，可能其部分内容已经发生变化，如有疑问可询问作者。

算法学习笔记(9): 后缀数组

定义

后缀数组是对后缀的一个排序，每个后缀按照字典序进行排序，然后用两个数组来映射它们自己和它们的排名。

同时，为了便于记录后缀，我们记字符串s的后缀s[i:]记为i，同时i和它的排名rank相互映射。这就是后缀数组。为了便于理解，在本文将此数组称为映射，这是它实际完成的任务，只是数组恰好作为这个工具。我们通常使用sa(rankToId) 和 rk(idToRank)两个映射来记录后缀数组。

如何构造后缀数组

做法一：暴力法

复杂度：O(n^2logn)

暴力排序，枚举出所有的后缀，在对所有的后缀进行排序。

做法二：倍增法

复杂度：O(nlog^2n)

为了完成这个思想，先建设一个前提，首先要了解字典排序的特点，当被排序的两者长度不一时。

当abc和b进行排序和123和2进行排序是不同的，进行等价的转换，实际上是123和200之间进行排序。虽然后缀的长度不同，实际上比较的时候，它们的长度是相同的。

如果所有后缀都要进行排序，不妨我们让短一点的后缀在后面填充0，好了，这下子所有后缀的长度都一样了。

这个算法的第一步：

首先对字符串s的所有长度为1的子串，即每个字符进行排序，得到排序后的编号数组sa1和排名数组 rk1。（此时如果有两者一样，两者的排名相同）

你就可以发现，对于他们的排序就相当于对每个后缀的第一个字符进行预先比较，下一步，就是这些预先比较使用动态规划的思想被后面的排序利用到。

再换一个角度去想，abac变成1213实际上就是一种序号编码，通过他们的大小进行了一个编码。

第二步，对所有长度为2的子串进行排序，此时，最后一位就是以0结尾。同时，依据这个思路，把长度为2 的子串进行了编码。但又是怎么排序的呢，位置1的取1和2，位置2的取2和3。

第三步，对所有长度为4的子串进行排序，注意！为什么从2直接跳跃到4，因为原来长度为2的情况已经被编码过了，将两个组合起来在进行排序就可以获得长度为4的排序。

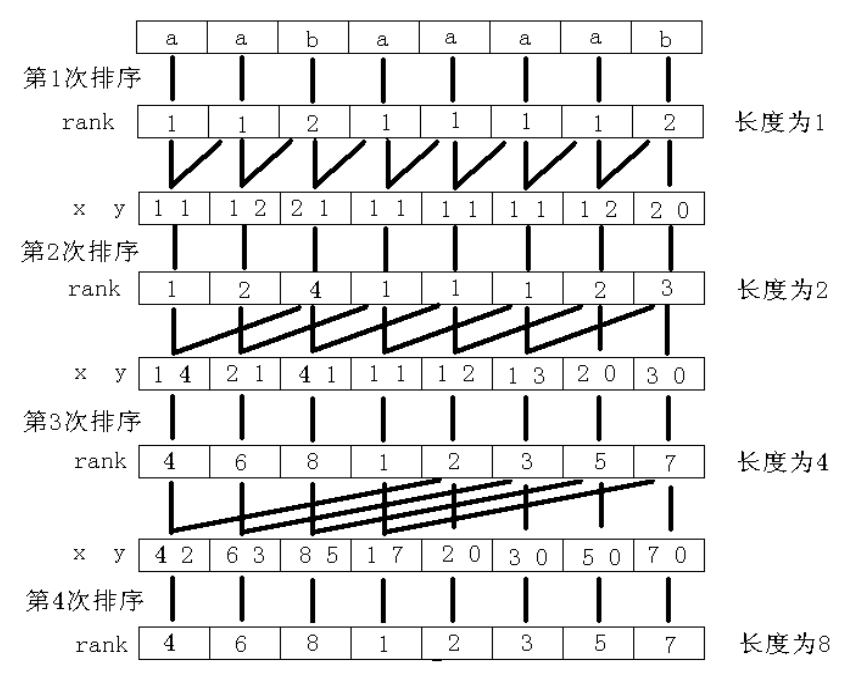
复杂度分析也就简单了，因为倍增所以排序logN次，每次排序消耗NlogN次。

void buildSAArray(const string& input){
	int len = input.size();
	vector<int> idToRank(2 * len);
	vector<int> RankToid(len + 1); // 由于没有第0名这个概念，于是空置第一个位置

	int currentSortLen;

    for (int i = 1; i <= len; ++i){
        RankToid[i] = i; // 塞入所有的名次编号
        idToRank[i] = input[i - 1];
        // 因为一开始未编码，所以只要保存大小关系即可，ascii能说明字典序
    }
	
	auto cmp = [&](int id1, int id2){
		if(idToRank[id1] == idToRank[id2]){
			return idToRank[id1 + currentSortLen] < idToRank[id2 + currentSortLen];
		}else{
			return idToRank[id1] < idToRank[id2];
		}
	};
	
	for(currentSortLen = 1; currentSortLen < len; currentSortLen <<= 1){
		sort(RankToid.begin() + 1, RankToid.end(), cmp);
		vector<int> temp(idToRank.begin(), idToRank.end());
		// 根据排序顺序编码化
		for (int p = 0, i = 1; i <= len; ++i) {
			if (temp[RankToid[i]] == temp[RankToid[i - 1]] and 
					temp[RankToid[i] + currentSortLen] == temp[RankToid[i - 1] + currentSortLen]) {
				idToRank[RankToid[i]] = p;
			} else {
				idToRank[RankToid[i]] = ++p;
			} 
	  }
	}
	// for (int i = 1; i <= len; ++i) printf("%d ", RankToid[i]);
  // cout << endl;
	// for (int i = 1; i <= len; ++i) printf("%d ", idToRank[i]);
  // 得到的RankToid和idToRank可自行选择方式返回获取
}

优化排序

此处可以选择优化的排序，使排序从NLogN提升到N，这样复杂度就会降低到NLogN。

通过做法2的思路，我们可以发现，我们的排序实际上被排序的元素只有两个标签值，称作双关键字。对此我们可以使用非比较排序的基数排序。

在进行基数排序之前，需要了解基数排序和计数排序的基本内容。它们都属于非比较排序。

计数排序

非比较排序就是不会进行元素之间的比较，计数排序使用了从空间角度上很暴力的手段。举一个例子就可以知道了。

对于排序序列 2 3 3 1 4 2 8

计数排序直接维护一个大数组，此处可以取长度为10。记录所有0~9的元素出现个数，然后再从小到大依次输出记录的个数。

此处记录了①有1个 ② 有2个 ③有2个④有2个⑧有1个。其余都是0个。按照顺序输出也就是

1 2 2 3 3 4 4 8

排序完成。

基数排序

基数排序适用于多关键字排序，对于自然数来说，关键字就是不同的例如百位十位个位的值，而这个双关键字的情况，根据MSD 基数排序, 也就是从小的位到大的位进行排序。再结合计数排序，先按照第二关键字进行计数排序，取出所有，再对第一关键字进行排序即可。

以下就是基于基数排序的使排序复杂度降低到O(N)

void buildSAArray(const string& input) {
	int len = input.size();
	vector<int> idToRank(2 * len);
	vector<int> rankToid(len + 1);

	int currentSortLen;
	
	vector<int> cnt(128);
	for(int i = 1; i <= len; i++){ // 此处就是计数排序
		idToRank[i] = input[i - 1];
		cnt[input[i - 1]]++;
	}
	
	for(int i = 1; i <= cnt.size() - 1; i++){
		// 计算前缀和的原因是，我们需要的并不是计数排序输出所有元素，而是获取排名。
		cnt[i] += cnt[i - 1];
	} 

	for(int i = len; i >= 1; i--){
        // 放在SA里面的排名也就是index 需要不一样，所以这里要减一
        int rank = cnt[input[i - 1]];
        cnt[input[i - 1]]--;
		rankToid[rank] = i;
    }
    vector<int> oldIdToRank(idToRank);
	
    // 排名序列化，之前说明过
    for (int p = 0, i = 1; i <= len; ++i) {
        if (oldIdToRank[rankToid[i]] == oldIdToRank[rankToid[i - 1]]) {
        idToRank[rankToid[i]] = p;
        } else {
        idToRank[rankToid[i]] = ++p;
        }
    }

    for (currentSortLen = 1; currentSortLen < len; currentSortLen <<= 1) {
        // 对第二关键字：idToRank[RankToid[i] + currentSortLen]进行计数排序
        vector<int> cnt(len + 1);
        vector<int> id(rankToid); // id保存一份儿RankToid的拷贝，实质上就相当于oldRankToid
        
        for (int i = 1; i <= len; ++i){
            int secondValue = idToRank[id[i] + currentSortLen];
            cnt[secondValue]++;
        }

        for (int i = 1; i <= cnt.size() - 1; ++i) {
            // 进行前缀和，理由和上面一样
            cnt[i] += cnt[i - 1];
        }

        for(int i = len; i >= 1; i--){
            int secondValue = idToRank[id[i] + currentSortLen];
            int rank = cnt[secondValue];
            cnt[secondValue]--;
            rankToid[rank] = id[i];
        }

        // 对第一关键字：id[i]进行计数排序
        fill(cnt.begin(), cnt.end(), 0);

        id = rankToid;

        for (int i = 1; i <= len; ++i){
            int firstValue = idToRank[id[i]];
            cnt[firstValue]++;
        }

        for(int i = 1; i <= len; i++){
            cnt[i] += cnt[i - 1];
        }

        for(int i = len; i >= 1; i--){
            int firstValue = idToRank[id[i]];
            int rank = cnt[firstValue];
            cnt[firstValue] --;
            rankToid[rank] = id[i];
        }

        // 以上的两次计数排序就完成了一次基数排序
        vector<int> oldidToRank(idToRank);
        for (int p = 0, i = 1; i <= len; ++i) {
            if (oldidToRank[rankToid[i]] == oldidToRank[rankToid[i - 1]] &&
                oldidToRank[rankToid[i] + currentSortLen] == oldidToRank[rankToid[i - 1] + currentSortLen]) {
                idToRank[rankToid[i]] = p;
            } else {
                idToRank[rankToid[i]] = ++p;
            }
        }
    }

    for (int i = 1; i <= len; ++i) printf("%d ", rankToid[i]);
}

根据以上代码的重新整理和总结，简化了许多以及使人更容易看懂。以下是一些注意点：

在进行SA构建的中途idToRank和rankToid是不一定互相映射的，因为rankToId的index作为rank，rank是唯一的，然后idToRank中，如果两者一样，排名也会一样。至于为什么最后还是相互映射的，因为所有的后缀长度不一样，所以必定不会出现相同的情况。

一开始的时候，idToRank并不是真正意义上的rank，实际上包括在过程中，rank的作用只需要是能体现两者之间的大小关系就可以。在每次排完后，会进行一次序列化，就会变成从1开始的排名。

以上代码仅供参考理解，性能方面不敢保证，理解算法本质后可使用他人模板。

常数优化

第二关键字排序优化

第二关键字实际上是偏移后的位置，因为上面的考虑，第二关键字很多时候都是空，也就是等同于0的存在。对于计数排序，在计数完后再取出进行编号就会变得不那么必要了，因为它为0，就必定先出，可以直接进行序列化编号。

优化计数排序的范围

计数排序的缺点在于空间的使用以及需要遍历空间，然而我们说过，一旦出现相同，rank值可以一样，又因为计数排序的容器大小就是被排序元素种类的个数，所以有的时候不一定为len，可以用p获取种类数进行优化。

将 相互映射 保存

因为计算过程中的映射不统一，所以计算中经常出现idToRank[rankToid[i]]，可以直接保存这个关系，减少不连续内存访问

用函数替换重复判断

把 oldrk[sa[i]] == oldrk[sa[i - 1]] && oldrk[sa[i] + w] == oldrk[sa[i - 1] + w]

替换成 cmp(sa[i], sa[i - 1], w)，

bool cmp(int x, int y, int w) { return oldrk[x] == oldrk[y] && oldrk[x + w] == oldrk[y + w]; }。

若排名都不相同可直接生成后缀数组

如果过程中，排名已经没有出现重复，那么实际上已经排序结束了。

O(N) 参考

SA-IS

可以参考 诱导排序与 SA-IS 算法，另外它的 评论页面 也有参考价值。

DC3

可以参考[2009] 后缀数组——处理字符串的有力工具 by. 罗穗骞。

后缀数组的应用

后缀数组通常和子串有关，因为子串实际上就是后缀的前缀。例如**在字符串中找子串，**因为有了后缀数组，可以直接二分去找。或者是利用好单调性，同时关注前缀关键词，有的时候，题目的前缀也就是反串的后缀。

用后缀数组构建height 数组

LCP（最长公共前缀）：lcp(i, j) 后缀i和后缀j的最长公共前缀（的长度） height[i] = lcp(sa[i], sa[i - 1])

易得

height[rank[i]] ≥ height[rank[i - 1]] - 1

for (i = 1, k = 0; i <= n; ++i) {
  if (rk[i] == 0) continue;
  if (k) --k;
  while (s[i + k] == s[sa[rk[i] - 1] + k]) ++k;
  height[rk[i]] = k;
}

height 数组应用

两子串最长公共前缀

lcp(sa[i], sa[j]) = min(height[i + 1 ~ j])

区间最值问题

比较一个字符串的两个子串的大小关系

设A = S[a~b] , B = S[c~d]

if lcp(a, c) ≥ min(|A|, |B|) ， A < B = |A| < |B|

else A < B = rk[a] < rk[c]

不同子串的数目

答案是n(n +1) / 2 - sum(height[2:])

出现至少 k 次的子串的最大长度

出现至少k次意味着后缀排序后有至少连续k个后缀以这个子串作为公共前缀。所以，求出每相邻k个的最小值，再求这些最小值的最大值就是答案。

某字符串在文本串中至少不重叠地出现了两次

可以二分目标串的长度|s|，将h数组划分成若干个连续 LCP 大于等于 |s| 的段，利用 RMQ 对每个段求其中出现的数中最大和最小的下标，若这两个下标的距离满足条件，则一定有长度为 |s| 的字符串不重叠地出现了两次。